LeetCode in Kotlin

3650. Minimum Cost Path with Edge Reversals

Medium

You are given a directed, weighted graph with n nodes labeled from 0 to n - 1, and an array edges where edges[i] = [ui, vi, wi] represents a directed edge from node ui to node vi with cost wi.

Each node ui has a switch that can be used at most once: when you arrive at ui and have not yet used its switch, you may activate it on one of its incoming edges vi → ui reverse that edge to ui → vi and immediately traverse it.

The reversal is only valid for that single move, and using a reversed edge costs 2 * wi.

Return the minimum total cost to travel from node 0 to node n - 1. If it is not possible, return -1.

Example 1:

Input: n = 4, edges = [[0,1,3],[3,1,1],[2,3,4],[0,2,2]]

Output: 5

Explanation:

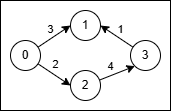
• Use the path 0 → 1 (cost 3).
• At node 1 reverse the original edge 3 → 1 into 1 → 3 and traverse it at cost 2 * 1 = 2.
• Total cost is 3 + 2 = 5.

Example 2:

Input: n = 4, edges = [[0,2,1],[2,1,1],[1,3,1],[2,3,3]]

Output: 3

Explanation:

• No reversal is needed. Take the path 0 → 2 (cost 1), then 2 → 1 (cost 1), then 1 → 3 (cost 1).
• Total cost is 1 + 1 + 1 = 3.

Constraints:

• 2 <= n <= 5 * 104
• 1 <= edges.length <= 105
• edges[i] = [ui, vi, wi]
• 0 <= ui, vi <= n - 1
• 1 <= wi <= 1000

Solution

import java.util.PriorityQueue

class Solution {
    private var cnt = 0
    private lateinit var head: IntArray
    private lateinit var next: IntArray
    private lateinit var to: IntArray
    private lateinit var weight: IntArray

    private class Dist(var u: Int, var d: Int) : Comparable<Dist> {
        override fun compareTo(other: Dist): Int {
            return d.toLong().compareTo(other.d.toLong())
        }
    }

    private fun init(n: Int, m: Int) {
        head = IntArray(n)
        head.fill(-1)
        next = IntArray(m)
        to = IntArray(m)
        weight = IntArray(m)
    }

    private fun add(u: Int, v: Int, w: Int) {
        to[cnt] = v
        weight[cnt] = w
        next[cnt] = head[u]
        head[u] = cnt++
    }

    private fun dist(s: Int, t: Int, n: Int): Int {
        val queue: PriorityQueue<Dist> = PriorityQueue<Dist>()
        val dist = IntArray(n)
        dist.fill(INF)
        dist[s] = 0
        queue.add(Dist(s, dist[s]))
        while (queue.isNotEmpty()) {
            val d = queue.remove()
            val u = d.u
            if (dist[u] < d.d) {
                continue
            }
            if (u == t) {
                return dist[t]
            }
            var i = head[u]
            while (i != -1) {
                val v = to[i]
                val w = weight[i]
                if (dist[v] > dist[u] + w) {
                    dist[v] = dist[u] + w
                    queue.add(Dist(v, dist[v]))
                }
                i = next[i]
            }
        }
        return INF
    }

    fun minCost(n: Int, edges: Array<IntArray>): Int {
        val m = edges.size
        init(n, 2 * m)
        for (edge in edges) {
            val u = edge[0]
            val v = edge[1]
            val w = edge[2]
            add(u, v, w)
            add(v, u, 2 * w)
        }
        val ans = dist(0, n - 1, n)
        return if (ans == INF) -1 else ans
    }

    companion object {
        private const val INF = Int.Companion.MAX_VALUE / 2 - 1
    }
}

This site is open source. Improve this page.