LeetCode in Kotlin

3613. Minimize Maximum Component Cost

Medium

You are given an undirected connected graph with n nodes labeled from 0 to n - 1 and a 2D integer array edges where edges[i] = [ui, vi, wi] denotes an undirected edge between node ui and node vi with weight wi, and an integer k.

You are allowed to remove any number of edges from the graph such that the resulting graph has at most k connected components.

The cost of a component is defined as the maximum edge weight in that component. If a component has no edges, its cost is 0.

Return the minimum possible value of the maximum cost among all components after such removals.

Example 1:

Input: n = 5, edges = [[0,1,4],[1,2,3],[1,3,2],[3,4,6]], k = 2

Output: 4

Explanation:

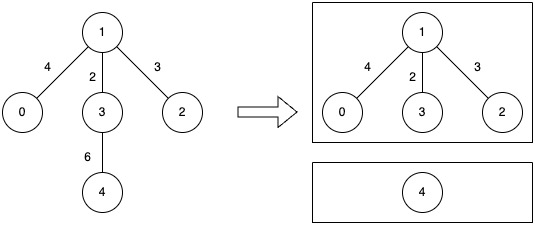
• Remove the edge between nodes 3 and 4 (weight 6).
• The resulting components have costs of 0 and 4, so the overall maximum cost is 4.

Example 2:

Input: n = 4, edges = [[0,1,5],[1,2,5],[2,3,5]], k = 1

Output: 5

Explanation:

• No edge can be removed, since allowing only one component (k = 1) requires the graph to stay fully connected.
• That single component’s cost equals its largest edge weight, which is 5.

Constraints:

• 1 <= n <= 5 * 104
• 0 <= edges.length <= 105
• edges[i].length == 3
• 0 <= ui, vi < n
• 1 <= wi <= 106
• 1 <= k <= n
• The input graph is connected.

Solution

import kotlin.math.max

class Solution {
    fun minCost(ui: Int, pl: Array<IntArray>, zx: Int): Int {
        var rt = 0
        var gh = 0
        var i = 0
        while (i < pl.size) {
            gh = max(gh, pl[i][2])
            i++
        }
        while (rt < gh) {
            val ty = rt + (gh - rt) / 2
            if (dfgh(ui, pl, ty, zx)) {
                gh = ty
            } else {
                rt = ty + 1
            }
        }
        return rt
    }

    private fun dfgh(ui: Int, pl: Array<IntArray>, jk: Int, zx: Int): Boolean {
        val wt = IntArray(ui)
        var i = 0
        while (i < ui) {
            wt[i] = i
            i++
        }
        var er = ui
        i = 0
        while (i < pl.size) {
            val df = pl[i]
            if (df[2] > jk) {
                i++
                continue
            }
            val u = cvb(wt, df[0])
            val v = cvb(wt, df[1])
            if (u != v) {
                wt[u] = v
                er--
            }
            i++
        }
        return er <= zx
    }

    private fun cvb(wt: IntArray, i: Int): Int {
        var i = i
        while (wt[i] != i) {
            wt[i] = wt[wt[i]]
            i = wt[i]
        }
        return i
    }
}

This site is open source. Improve this page.