LeetCode in Kotlin

3588. Find Maximum Area of a Triangle

Medium

You are given a 2D array coords of size n x 2, representing the coordinates of n points in an infinite Cartesian plane.

Find twice the maximum area of a triangle with its corners at any three elements from coords, such that at least one side of this triangle is parallel to the x-axis or y-axis. Formally, if the maximum area of such a triangle is A, return 2 * A.

If no such triangle exists, return -1.

Note that a triangle cannot have zero area.

Example 1:

Input: coords = [[1,1],[1,2],[3,2],[3,3]]

Output: 2

Explanation:

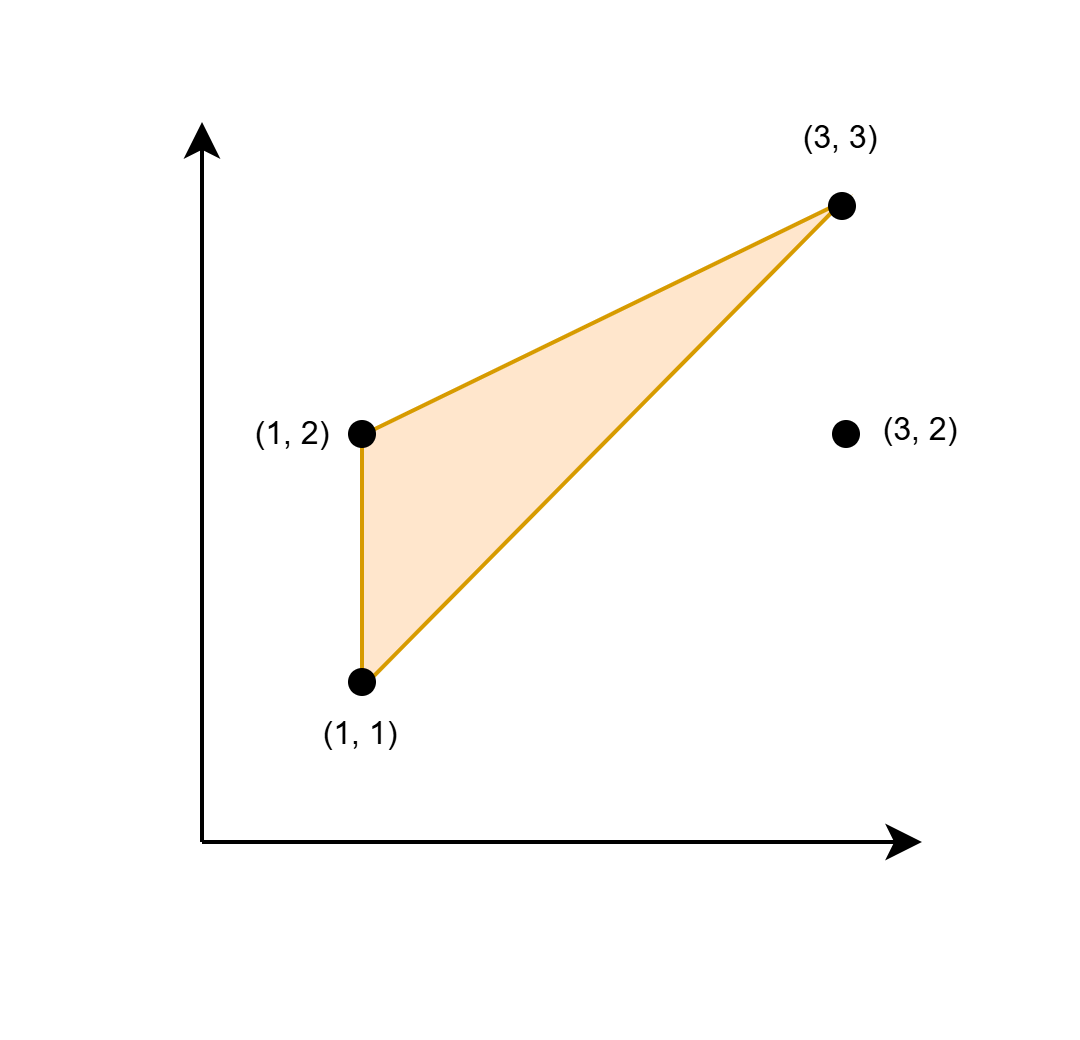
The triangle shown in the image has a base 1 and height 2. Hence its area is 1/2 * base * height = 1.

Example 2:

Input: coords = [[1,1],[2,2],[3,3]]

Output: -1

Explanation:

The only possible triangle has corners (1, 1), (2, 2), and (3, 3). None of its sides are parallel to the x-axis or the y-axis.

Constraints:

• 1 <= n == coords.length <= 105
• 1 <= coords[i][0], coords[i][1] <= 106
• All coords[i] are unique.

Solution

import java.util.TreeSet
import kotlin.math.abs
import kotlin.math.max

class Solution {
    fun maxArea(coords: Array<IntArray>): Long {
        val xMap: MutableMap<Int, TreeSet<Int>> = HashMap<Int, TreeSet<Int>>()
        val yMap: MutableMap<Int, TreeSet<Int>> = HashMap<Int, TreeSet<Int>>()
        val allX = TreeSet<Int>()
        val allY = TreeSet<Int>()
        for (coord in coords) {
            val x = coord[0]
            val y = coord[1]
            xMap.computeIfAbsent(x) { _: Int -> TreeSet<Int>() }.add(y)
            yMap.computeIfAbsent(y) { _: Int -> TreeSet<Int>() }.add(x)
            allX.add(x)
            allY.add(y)
        }
        var ans = Long.Companion.MIN_VALUE
        for (entry in xMap.entries) {
            val x: Int = entry.key
            val ySet: TreeSet<Int> = entry.value
            if (ySet.size < 2) {
                continue
            }
            val minY: Int = ySet.first()!!
            val maxY: Int = ySet.last()!!
            val base = maxY - minY
            val minX: Int = allX.first()!!
            val maxX: Int = allX.last()!!
            if (minX != x) {
                ans = max(ans, abs(x - minX).toLong() * base)
            }
            if (maxX != x) {
                ans = max(ans, abs(x - maxX).toLong() * base)
            }
        }

        for (entry in yMap.entries) {
            val y: Int = entry.key
            val xSet: TreeSet<Int> = entry.value
            if (xSet.size < 2) {
                continue
            }
            val minX: Int = xSet.first()!!
            val maxX: Int = xSet.last()!!
            val base = maxX - minX
            val minY: Int = allY.first()!!
            val maxY: Int = allY.last()!!
            if (minY != y) {
                ans = max(ans, abs(y - minY).toLong() * base)
            }
            if (maxY != y) {
                ans = max(ans, abs(y - maxY).toLong() * base)
            }
        }
        return if (ans == Long.Companion.MIN_VALUE) -1 else ans
    }
}

This site is open source. Improve this page.