LeetCode in Kotlin

3585. Find Weighted Median Node in Tree

Hard

You are given an integer n and an undirected, weighted tree rooted at node 0 with n nodes numbered from 0 to n - 1. This is represented by a 2D array edges of length n - 1, where edges[i] = [ui, vi, wi] indicates an edge from node ui to vi with weight wi.

The weighted median node is defined as the first node x on the path from ui to vi such that the sum of edge weights from ui to x is greater than or equal to half of the total path weight.

You are given a 2D integer array queries. For each queries[j] = [uj, vj], determine the weighted median node along the path from uj to vj.

Return an array ans, where ans[j] is the node index of the weighted median for queries[j].

Example 1:

Input: n = 2, edges = [[0,1,7]], queries = [[1,0],[0,1]]

Output: [0,1]

Explanation:

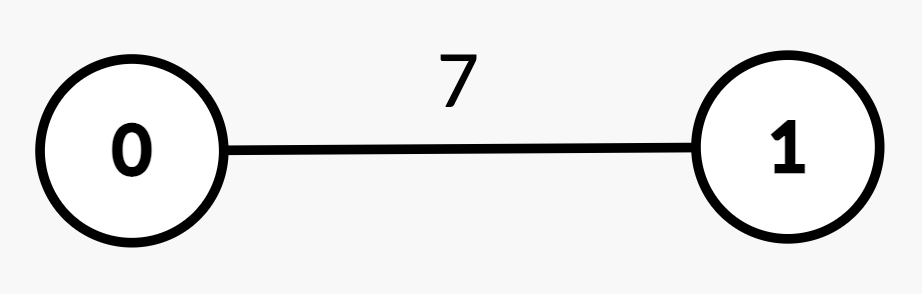
Query Path Edge Weights Total Path Weight Half Explanation Answer
[1, 0] 1 → 0 [7] 7 3.5 Sum from 1 → 0 = 7 >= 3.5, median is node 0. 0
[0, 1] 0 → 1 [7] 7 3.5 Sum from 0 → 1 = 7 >= 3.5, median is node 1. 1

Example 2:

Input: n = 3, edges = [[0,1,2],[2,0,4]], queries = [[0,1],[2,0],[1,2]]

Output: [1,0,2]

Explanation:

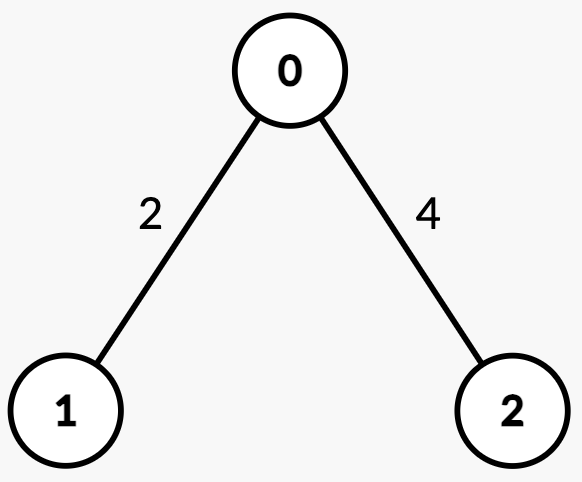
Query Path Edge Weights Total Path Weight Half Explanation Answer
[0, 1] 0 → 1 [2] 2 1 Sum from 0 → 1 = 2 >= 1, median is node 1. 1
[2, 0] 2 → 0 [4] 4 2 Sum from 2 → 0 = 4 >= 2, median is node 0. 0
[1, 2] 1 → 0 → 2 [2, 4] 6 3 Sum from 1 → 0 = 2 < 3.
Sum from 1 → 2 = 2 + 4 = 6 >= 3, median is node 2.		 2

Example 3:

Input: n = 5, edges = [[0,1,2],[0,2,5],[1,3,1],[2,4,3]], queries = [[3,4],[1,2]]

Output: [2,2]

Explanation:

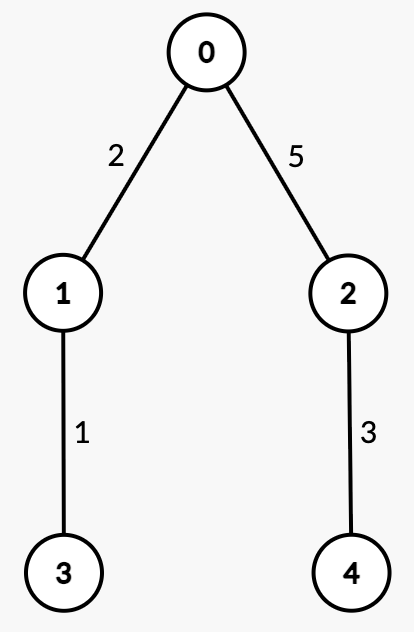
Query Path Edge Weights Total Path Weight Half Explanation Answer
[3, 4] 3 → 1 → 0 → 2 → 4 [1, 2, 5, 3] 11 5.5 Sum from 3 → 1 = 1 < 5.5.
Sum from 3 → 0 = 1 + 2 = 3 < 5.5.
Sum from 3 → 2 = 1 + 2 + 5 = 8 >= 5.5, median is node 2.		 2
[1, 2] 1 → 0 → 2 [2, 5] 7 3.5 Sum from 1 → 0 = 2 < 3.5.
Sum from 1 → 2 = 2 + 5 = 7 >= 3.5, median is node 2.		 2

Constraints:

Solution

import kotlin.math.ceil
import kotlin.math.ln

class Solution {
    private lateinit var adj: MutableList<MutableList<IntArray>>
    private lateinit var depth: IntArray
    private lateinit var dist: LongArray
    private lateinit var parent: Array<IntArray>
    private var longMax = 0
    private var nodes = 0

    fun findMedian(n: Int, edges: Array<IntArray>, queries: Array<IntArray>): IntArray {
        nodes = n
        if (n > 1) {
            longMax = ceil(ln(n.toDouble()) / ln(2.0)).toInt()
        } else {
            longMax = 1
        }
        adj = ArrayList()
        for (i in 0..<n) {
            adj.add(ArrayList())
        }
        for (edge in edges) {
            val u = edge[0]
            val v = edge[1]
            val w = edge[2]
            adj[u].add(intArrayOf(v, w))
            adj[v].add(intArrayOf(u, w))
        }
        depth = IntArray(n)
        dist = LongArray(n)
        parent = Array(longMax) { IntArray(n) }
        for (i in 0..<longMax) {
            parent[i].fill(-1)
        }
        dfs(0, -1, 0, 0L)
        buildLcaTable()
        val ans = IntArray(queries.size)
        var sabrelonta: IntArray
        for (qIdx in queries.indices) {
            sabrelonta = queries[qIdx]
            val u = sabrelonta[0]
            val v = sabrelonta[1]
            ans[qIdx] = findMedianNode(u, v)
        }

        return ans
    }

    private fun dfs(u: Int, p: Int, d: Int, currentDist: Long) {
        depth[u] = d
        parent[0][u] = p
        dist[u] = currentDist
        for (edge in adj[u]) {
            val v = edge[0]
            val w = edge[1]
            if (v == p) {
                continue
            }
            dfs(v, u, d + 1, currentDist + w)
        }
    }

    private fun buildLcaTable() {
        for (k in 1..<longMax) {
            for (node in 0..<nodes) {
                if (parent[k - 1][node] != -1) {
                    parent[k][node] = parent[k - 1][parent[k - 1][node]]
                }
            }
        }
    }

    private fun getKthAncestor(u: Int, k: Int): Int {
        var u = u
        for (p in longMax - 1 downTo 0) {
            if (u == -1) {
                break
            }
            if (((k shr p) and 1) == 1) {
                u = parent[p][u]
            }
        }
        return u
    }

    private fun getLCA(u: Int, v: Int): Int {
        var u = u
        var v = v
        if (depth[u] < depth[v]) {
            val temp = u
            u = v
            v = temp
        }
        u = getKthAncestor(u, depth[u] - depth[v])
        if (u == v) {
            return u
        }
        for (p in longMax - 1 downTo 0) {
            if (parent[p][u] != -1 && parent[p][u] != parent[p][v]) {
                u = parent[p][u]
                v = parent[p][v]
            }
        }
        return parent[0][u]
    }

    private fun findMedianNode(u: Int, v: Int): Int {
        if (u == v) {
            return u
        }
        val lca = getLCA(u, v)
        val totalPathWeight = dist[u] + dist[v] - 2 * dist[lca]
        val halfWeight = (totalPathWeight + 1) / 2L
        return if (dist[u] - dist[lca] >= halfWeight) {
            var curr = u
            for (p in longMax - 1 downTo 0) {
                val nextNode = parent[p][curr]
                if (nextNode != -1 && (dist[u] - dist[nextNode] < halfWeight)) {
                    curr = nextNode
                }
            }
            parent[0][curr]
        } else {
            val remainingWeightFromLCA = halfWeight - (dist[u] - dist[lca])
            var curr = v
            for (p in longMax - 1 downTo 0) {
                val nextNode = parent[p][curr]
                if (nextNode != -1 && depth[nextNode] >= depth[lca] &&
                    (dist[nextNode] - dist[lca]) >= remainingWeightFromLCA
                ) {
                    curr = nextNode
                }
            }
            curr
        }
    }
}
This site is open source. Improve this page.