LeetCode in Kotlin

3575. Maximum Good Subtree Score

Hard

You are given an undirected tree rooted at node 0 with n nodes numbered from 0 to n - 1. Each node i has an integer value vals[i], and its parent is given by par[i].

A subset of nodes within the subtree of a node is called good if every digit from 0 to 9 appears at most once in the decimal representation of the values of the selected nodes.

The score of a good subset is the sum of the values of its nodes.

Define an array maxScore of length n, where maxScore[u] represents the maximum possible sum of values of a good subset of nodes that belong to the subtree rooted at node u, including u itself and all its descendants.

Return the sum of all values in maxScore.

Since the answer may be large, return it modulo 109 + 7.

Example 1:

Input: vals = [2,3], par = [-1,0]

Output: 8

Explanation:

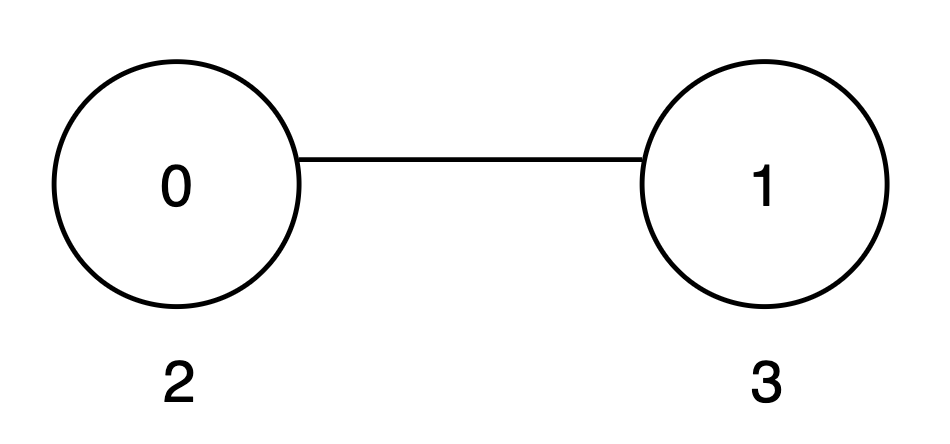
• The subtree rooted at node 0 includes nodes {0, 1}. The subset {2, 3} is good as the digits 2 and 3 appear only once. The score of this subset is 2 + 3 = 5.
• The subtree rooted at node 1 includes only node {1}. The subset {3} is good. The score of this subset is 3.
• The maxScore array is [5, 3], and the sum of all values in maxScore is 5 + 3 = 8. Thus, the answer is 8.

Example 2:

Input: vals = [1,5,2], par = [-1,0,0]

Output: 15

Explanation:

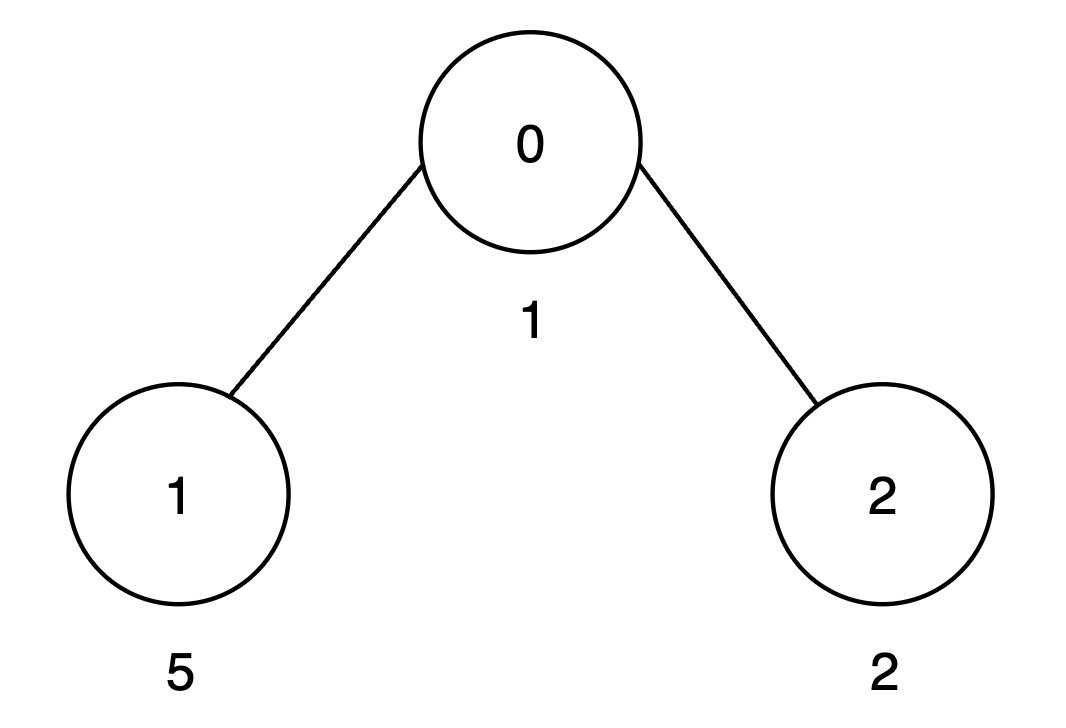
• The subtree rooted at node 0 includes nodes {0, 1, 2}. The subset {1, 5, 2} is good as the digits 1, 5 and 2 appear only once. The score of this subset is 1 + 5 + 2 = 8.
• The subtree rooted at node 1 includes only node {1}. The subset {5} is good. The score of this subset is 5.
• The subtree rooted at node 2 includes only node {2}. The subset {2} is good. The score of this subset is 2.
• The maxScore array is [8, 5, 2], and the sum of all values in maxScore is 8 + 5 + 2 = 15. Thus, the answer is 15.

Example 3:

Input: vals = [34,1,2], par = [-1,0,1]

Output: 42

Explanation:

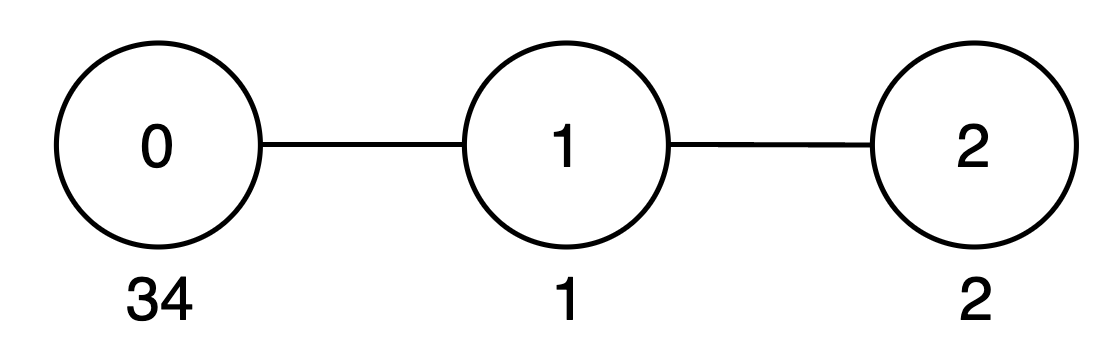
• The subtree rooted at node 0 includes nodes {0, 1, 2}. The subset {34, 1, 2} is good as the digits 3, 4, 1 and 2 appear only once. The score of this subset is 34 + 1 + 2 = 37.
• The subtree rooted at node 1 includes node {1, 2}. The subset {1, 2} is good as the digits 1 and 2 appear only once. The score of this subset is 1 + 2 = 3.
• The subtree rooted at node 2 includes only node {2}. The subset {2} is good. The score of this subset is 2.
• The maxScore array is [37, 3, 2], and the sum of all values in maxScore is 37 + 3 + 2 = 42. Thus, the answer is 42.

Example 4:

Input: vals = [3,22,5], par = [-1,0,1]

Output: 18

Explanation:

• The subtree rooted at node 0 includes nodes {0, 1, 2}. The subset {3, 22, 5} is not good, as digit 2 appears twice. Therefore, the subset {3, 5} is valid. The score of this subset is 3 + 5 = 8.
• The subtree rooted at node 1 includes nodes {1, 2}. The subset {22, 5} is not good, as digit 2 appears twice. Therefore, the subset {5} is valid. The score of this subset is 5.
• The subtree rooted at node 2 includes {2}. The subset {5} is good. The score of this subset is 5.
• The maxScore array is [8, 5, 5], and the sum of all values in maxScore is 8 + 5 + 5 = 18. Thus, the answer is 18.

Constraints:

• 1 <= n == vals.length <= 500
• 1 <= vals[i] <= 109
• par.length == n
• par[0] == -1
• 0 <= par[i] < n for i in [1, n - 1]
• The input is generated such that the parent array par represents a valid tree.

Solution

import kotlin.math.max

class Solution {
    private val digits = 10
    private val full = 1 shl digits
    private val neg = Long.Companion.MIN_VALUE / 4
    private val mod = 1e9.toLong() + 7
    private lateinit var tree: Array<ArrayList<Int>>
    private lateinit var `val`: IntArray
    private lateinit var mask: IntArray
    private lateinit var isOk: BooleanArray
    private var res: Long = 0

    fun goodSubtreeSum(vals: IntArray, par: IntArray): Int {
        val n = vals.size
        `val` = vals
        mask = IntArray(n)
        isOk = BooleanArray(n)
        for (i in 0..<n) {
            var m = 0
            var v = vals[i]
            var valid = true
            while (v > 0) {
                val d = v % 10
                if (((m shr d) and 1) == 1) {
                    valid = false
                    break
                }
                m = m or (1 shl d)
                v /= 10
            }
            mask[i] = m
            isOk[i] = valid
        }
        tree = Array(n) { initialCapacity: Int -> ArrayList(initialCapacity) }
        val root = 0
        for (i in 1..<n) {
            tree[par[i]].add(i)
        }
        dfs(root)
        return (res % mod).toInt()
    }

    private fun dfs(u: Int): LongArray {
        var dp = LongArray(full)
        dp.fill(neg)
        dp[0] = 0
        if (isOk[u]) {
            dp[mask[u]] = `val`[u].toLong()
        }
        for (v in tree[u]) {
            val child = dfs(v)
            val newDp = dp.copyOf(full)
            for (m1 in 0..<full) {
                if (dp[m1] < 0) {
                    continue
                }
                val remain = full - 1 - m1
                var m2 = remain
                while (m2 > 0) {
                    if (child[m2] < 0) {
                        m2 = (m2 - 1) and remain
                        continue
                    }
                    val newM = m1 or m2
                    newDp[newM] = max(newDp[newM], dp[m1] + child[m2])
                    m2 = (m2 - 1) and remain
                }
            }
            dp = newDp
        }
        var best: Long = 0
        for (v in dp) {
            best = max(best, v)
        }
        res = (res + best) % mod
        return dp
    }
}

This site is open source. Improve this page.