LeetCode in Kotlin

3548. Equal Sum Grid Partition II

Hard

You are given an m x n matrix grid of positive integers. Your task is to determine if it is possible to make either one horizontal or one vertical cut on the grid such that:

• Each of the two resulting sections formed by the cut is non-empty.
• The sum of elements in both sections is equal, or can be made equal by discounting at most one single cell in total (from either section).
• If a cell is discounted, the rest of the section must remain connected.

Return true if such a partition exists; otherwise, return false.

Note: A section is connected if every cell in it can be reached from any other cell by moving up, down, left, or right through other cells in the section.

Example 1:

Input: grid = [[1,4],[2,3]]

Output: true

Explanation:

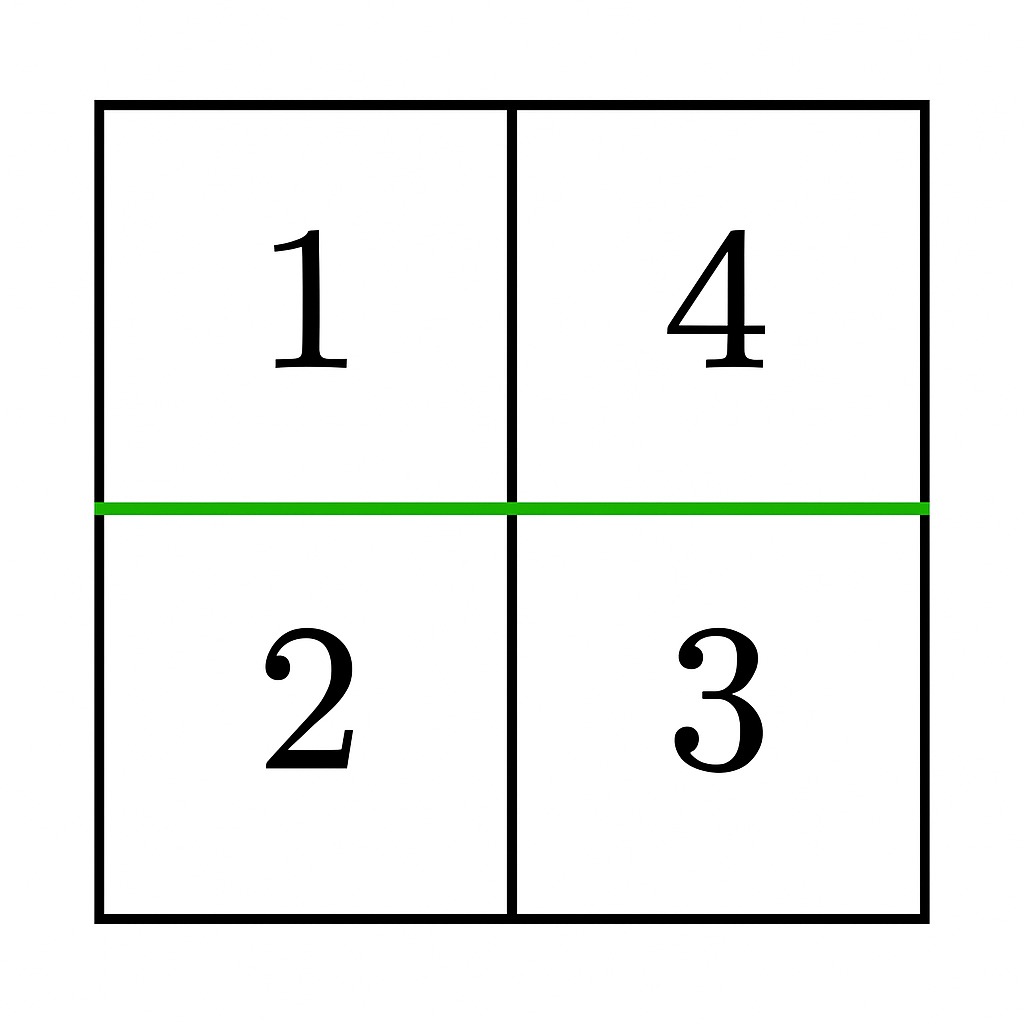
• A horizontal cut after the first row gives sums 1 + 4 = 5 and 2 + 3 = 5, which are equal. Thus, the answer is true.

Example 2:

Input: grid = [[1,2],[3,4]]

Output: true

Explanation:

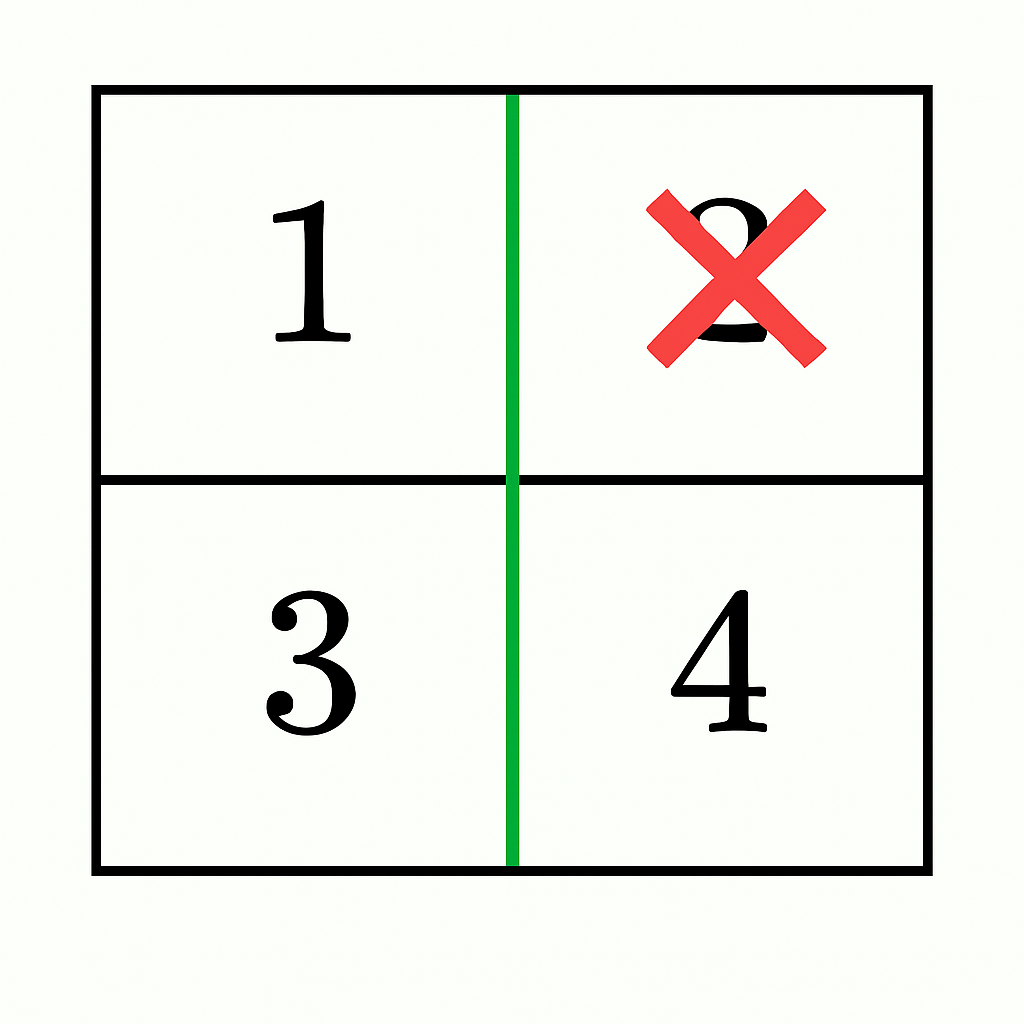
• A vertical cut after the first column gives sums 1 + 3 = 4 and 2 + 4 = 6.
• By discounting 2 from the right section (6 - 2 = 4), both sections have equal sums and remain connected. Thus, the answer is true.

Example 3:

Input: grid = [[1,2,4],[2,3,5]]

Output: false

Explanation:

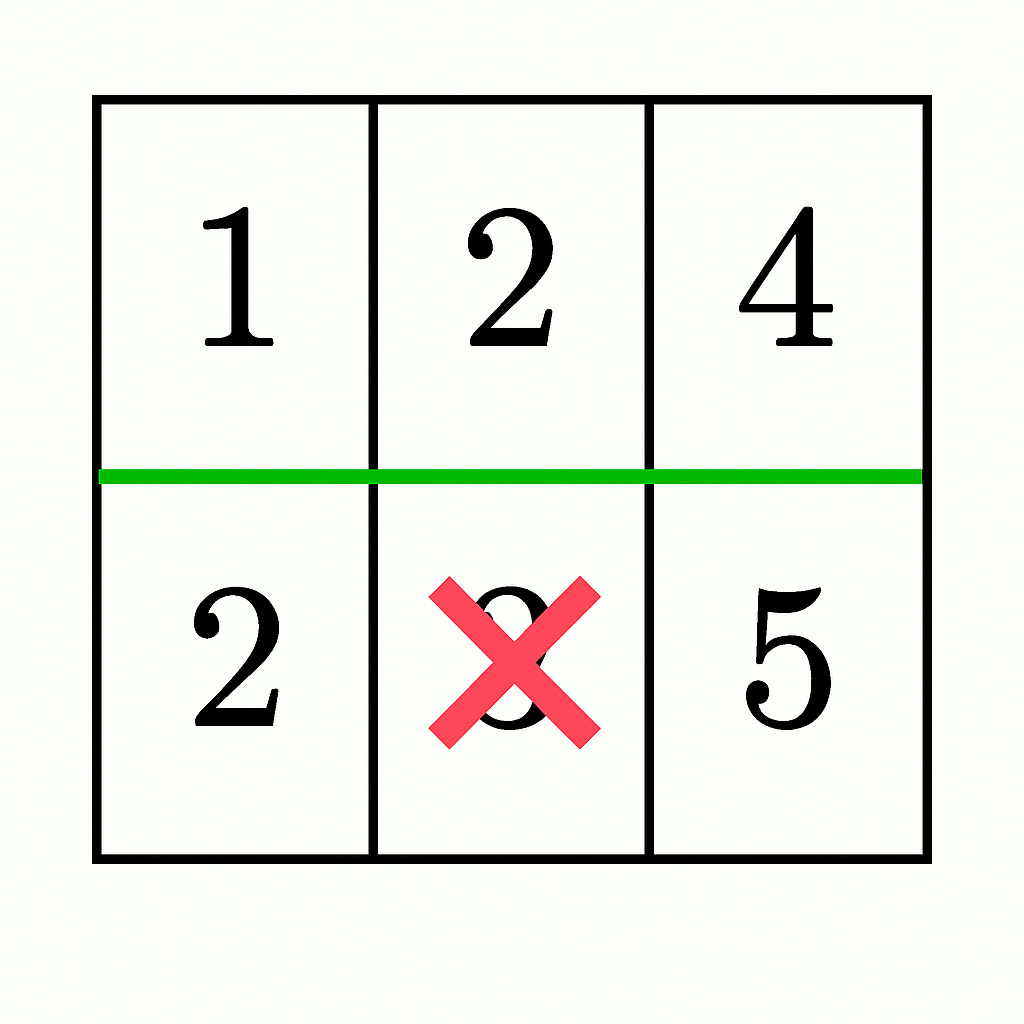
• A horizontal cut after the first row gives 1 + 2 + 4 = 7 and 2 + 3 + 5 = 10.
• By discounting 3 from the bottom section (10 - 3 = 7), both sections have equal sums, but they do not remain connected as it splits the bottom section into two parts ([2] and [5]). Thus, the answer is false.

Example 4:

Input: grid = [[4,1,8],[3,2,6]]

Output: false

Explanation:

No valid cut exists, so the answer is false.

Constraints:

• 1 <= m == grid.length <= 105
• 1 <= n == grid[i].length <= 105
• 2 <= m * n <= 105
• 1 <= grid[i][j] <= 105

Solution

class Solution {
    private fun calculateSum(grid: Array<IntArray>, count: IntArray): Long {
        var sum: Long = 0
        for (line in grid) {
            for (num in line) {
                sum += num.toLong()
                count[num]++
            }
        }
        return sum
    }

    private fun checkHorizontalPartition(grid: Array<IntArray>, sum: Long, count: IntArray): Boolean {
        val half = IntArray(MAX_SIZE)
        var now: Long = 0
        val m = grid.size
        val n = grid[0].size
        for (i in 0..<m - 1) {
            for (j in 0..<n) {
                now += grid[i][j].toLong()
                count[grid[i][j]]--
                half[grid[i][j]]++
            }
            if (now * 2 == sum) {
                return true
            }
            if (now * 2 > sum) {
                val diff = now * 2 - sum
                if (diff <= MAX_SIZE - 1 && half[diff.toInt()] > 0) {
                    if (n > 1) {
                        if (i > 0 || grid[0][0].toLong() == diff || grid[0][n - 1].toLong() == diff) {
                            return true
                        }
                    } else {
                        if (i > 0 && (grid[0][0].toLong() == diff || grid[i][0].toLong() == diff)) {
                            return true
                        }
                    }
                }
            } else {
                val diff = sum - now * 2
                if (diff <= MAX_SIZE - 1 && count[diff.toInt()] > 0) {
                    if (n > 1) {
                        if (i < m - 2 || grid[m - 1][0].toLong() == diff || grid[m - 1][n - 1].toLong() == diff) {
                            return true
                        }
                    } else {
                        if (i > 0 && (grid[m - 1][0].toLong() == diff || grid[i + 1][0].toLong() == diff)) {
                            return true
                        }
                    }
                }
            }
        }
        return false
    }

    private fun checkVerticalPartition(grid: Array<IntArray>, sum: Long): Boolean {
        val count = IntArray(MAX_SIZE)
        val half = IntArray(MAX_SIZE)
        for (line in grid) {
            for (num in line) {
                count[num]++
            }
        }
        var now: Long = 0
        val m = grid.size
        val n = grid[0].size
        for (i in 0..<n - 1) {
            for (ints in grid) {
                now += ints[i].toLong()
                count[ints[i]]--
                half[ints[i]]++
            }
            if (now * 2 == sum) {
                return true
            }
            if (now * 2 > sum) {
                val diff = now * 2 - sum
                if (diff <= MAX_SIZE - 1 && half[diff.toInt()] > 0) {
                    if (m > 1) {
                        if (i > 0 || grid[0][0].toLong() == diff || grid[m - 1][0].toLong() == diff) {
                            return true
                        }
                    } else {
                        if (i > 0 && (grid[0][0].toLong() == diff || grid[0][i].toLong() == diff)) {
                            return true
                        }
                    }
                }
            } else {
                val diff = sum - now * 2
                if (diff <= MAX_SIZE - 1 && count[diff.toInt()] > 0) {
                    if (m > 1) {
                        if (i < n - 2 || grid[0][n - 1].toLong() == diff || grid[m - 1][n - 1].toLong() == diff) {
                            return true
                        }
                    } else {
                        if (i > 0 && (grid[0][n - 1].toLong() == diff || grid[0][i + 1].toLong() == diff)) {
                            return true
                        }
                    }
                }
            }
        }
        return false
    }

    fun canPartitionGrid(grid: Array<IntArray>): Boolean {
        val count = IntArray(MAX_SIZE)
        val sum = calculateSum(grid, count)
        return checkHorizontalPartition(grid, sum, count) || checkVerticalPartition(grid, sum)
    }

    companion object {
        private const val MAX_SIZE = 100001
    }
}

This site is open source. Improve this page.