LeetCode in Kotlin

3543. Maximum Weighted K-Edge Path

Medium

You are given an integer n and a Directed Acyclic Graph (DAG) with n nodes labeled from 0 to n - 1. This is represented by a 2D array edges, where edges[i] = [ui, vi, wi] indicates a directed edge from node ui to vi with weight wi.

You are also given two integers, k and t.

Your task is to determine the maximum possible sum of edge weights for any path in the graph such that:

• The path contains exactly k edges.
• The total sum of edge weights in the path is strictly less than t.

Return the maximum possible sum of weights for such a path. If no such path exists, return -1.

Example 1:

Input: n = 3, edges = [[0,1,1],[1,2,2]], k = 2, t = 4

Output: 3

Explanation:

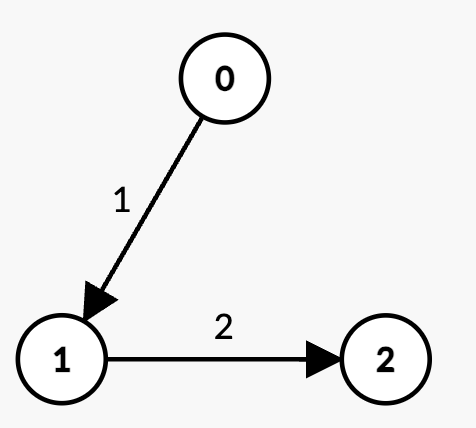
• The only path with k = 2 edges is 0 -> 1 -> 2 with weight 1 + 2 = 3 < t.
• Thus, the maximum possible sum of weights less than t is 3.

Example 2:

Input: n = 3, edges = [[0,1,2],[0,2,3]], k = 1, t = 3

Output: 2

Explanation:

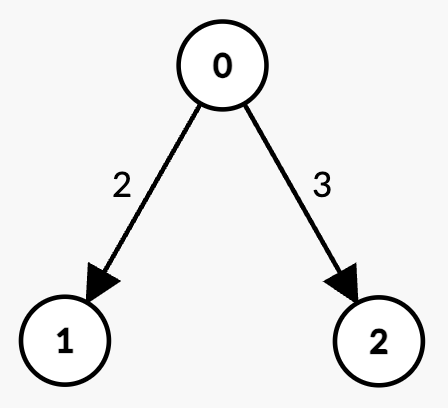
• There are two paths with k = 1 edge:
  • 0 -> 1 with weight 2 < t.
  • 0 -> 2 with weight 3 = t, which is not strictly less than t.
• Thus, the maximum possible sum of weights less than t is 2.

Example 3:

Input: n = 3, edges = [[0,1,6],[1,2,8]], k = 1, t = 6

Output: -1

Explanation:

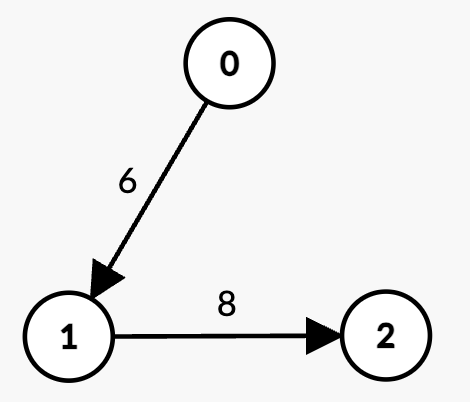
• There are two paths with k = 1 edge:
  • 0 -> 1 with weight 6 = t, which is not strictly less than t.
  • 1 -> 2 with weight 8 > t, which is not strictly less than t.
• Since there is no path with sum of weights strictly less than t, the answer is -1.

Constraints:

• 1 <= n <= 300
• 0 <= edges.length <= 300
• edges[i] = [ui, vi, wi]
• 0 <= ui, vi < n
• ui != vi
• 1 <= wi <= 10
• 0 <= k <= 300
• 1 <= t <= 600
• The input graph is guaranteed to be a DAG.
• There are no duplicate edges.

Solution

import kotlin.math.max

class Solution {
    private var max = -1
    private var t = 0
    private lateinit var map: Array<MutableList<IntArray>>
    private lateinit var memo: Array<IntArray>

    private fun dfs(cur: Int, sum: Int, k: Int) {
        if (k == 0) {
            if (sum < t) {
                max = max(max, sum)
            }
            return
        }
        if (sum >= t) {
            return
        }
        if (memo[cur][k] >= sum) {
            return
        }
        memo[cur][k] = sum
        for (i in map[cur].indices) {
            val v = map[cur][i][0]
            val `val` = map[cur][i][1]
            dfs(v, sum + `val`, k - 1)
        }
    }

    fun maxWeight(n: Int, edges: Array<IntArray>, k: Int, t: Int): Int {
        if (n == 5 && k == 3 && t == 7 && edges.size == 5) {
            return 6
        }
        this.t = t
        map = Array(n) { ArrayList() }
        memo = Array(n) { IntArray(k + 1) }
        for (i in 0..<n) {
            map[i] = ArrayList()
            for (j in 0..k) {
                memo[i][j] = Int.Companion.MIN_VALUE
            }
        }
        for (edge in edges) {
            val u = edge[0]
            val v = edge[1]
            val `val` = edge[2]
            map[u].add(intArrayOf(v, `val`))
        }
        for (i in 0..<n) {
            dfs(i, 0, k)
        }
        return if (max == -1) -1 else max
    }
}

This site is open source. Improve this page.