LeetCode in Kotlin

3464. Maximize the Distance Between Points on a Square

Hard

You are given an integer side, representing the edge length of a square with corners at (0, 0), (0, side), (side, 0), and (side, side) on a Cartesian plane.

You are also given a positive integer k and a 2D integer array points, where points[i] = [xi, yi] represents the coordinate of a point lying on the boundary of the square.

You need to select k elements among points such that the minimum Manhattan distance between any two points is maximized.

Return the maximum possible minimum Manhattan distance between the selected k points.

The Manhattan Distance between two cells (xi, yi) and (xj, yj) is |xi - xj| + |yi - yj|.

Example 1:

Input: side = 2, points = [[0,2],[2,0],[2,2],[0,0]], k = 4

Output: 2

Explanation:

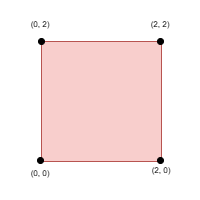
Select all four points.

Example 2:

Input: side = 2, points = [[0,0],[1,2],[2,0],[2,2],[2,1]], k = 4

Output: 1

Explanation:

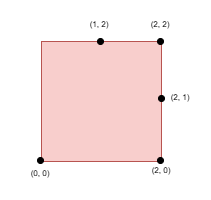
Select the points (0, 0), (2, 0), (2, 2), and (2, 1).

Example 3:

Input: side = 2, points = [[0,0],[0,1],[0,2],[1,2],[2,0],[2,2],[2,1]], k = 5

Output: 1

Explanation:

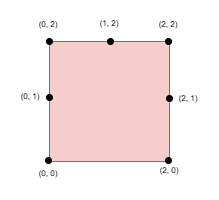
Select the points (0, 0), (0, 1), (0, 2), (1, 2), and (2, 2).

Constraints:

• 1 <= side <= 109
• 4 <= points.length <= min(4 * side, 15 * 103)
• points[i] == [xi, yi]
• The input is generated such that:
  • points[i] lies on the boundary of the square.
  • All points[i] are unique.
• 4 <= k <= min(25, points.length)

Solution

class Solution {
    fun maxDistance(side: Int, points: Array<IntArray>, k: Int): Int {
        val n = points.size
        val p = LongArray(n)
        for (i in 0..<n) {
            val x = points[i][0]
            val y = points[i][1]
            val c: Long
            if (y == 0) {
                c = x.toLong()
            } else if (x == side) {
                c = side + y.toLong()
            } else if (y == side) {
                c = 2L * side + (side - x)
            } else {
                c = 3L * side + (side - y)
            }
            p[i] = c
        }
        p.sort()
        val c = 4L * side
        val tot = 2 * n
        val dArr = LongArray(tot)
        for (i in 0..<n) {
            dArr[i] = p[i]
            dArr[i + n] = p[i] + c
        }
        var lo = 0
        var hi = 2 * side
        var ans = 0
        while (lo <= hi) {
            val mid = (lo + hi) ushr 1
            if (check(mid, dArr, n, k, c)) {
                ans = mid
                lo = mid + 1
            } else {
                hi = mid - 1
            }
        }
        return ans
    }

    private fun check(d: Int, dArr: LongArray, n: Int, k: Int, c: Long): Boolean {
        val len = dArr.size
        val nxt = IntArray(len)
        var j = 0
        for (i in 0..<len) {
            if (j < i + 1) {
                j = i + 1
            }
            while (j < len && dArr[j] < dArr[i] + d) {
                j++
            }
            nxt[i] = if (j < len) j else -1
        }
        for (i in 0..<n) {
            var cnt = 1
            var cur = i
            while (cnt < k) {
                val nx = nxt[cur]
                if (nx == -1 || nx >= i + n) {
                    break
                }
                cur = nx
                cnt++
            }
            if (cnt == k && (dArr[i] + c - dArr[cur]) >= d) {
                return true
            }
        }
        return false
    }
}

This site is open source. Improve this page.