LeetCode in Kotlin

3425. Longest Special Path

Hard

You are given an undirected tree rooted at node 0 with n nodes numbered from 0 to n - 1, represented by a 2D array edges of length n - 1, where edges[i] = [ui, vi, lengthi] indicates an edge between nodes ui and vi with length lengthi. You are also given an integer array nums, where nums[i] represents the value at node i.

A special path is defined as a downward path from an ancestor node to a descendant node such that all the values of the nodes in that path are unique.

Note that a path may start and end at the same node.

Return an array result of size 2, where result[0] is the length of the longest special path, and result[1] is the minimum number of nodes in all possible longest special paths.

Example 1:

Input: edges = [[0,1,2],[1,2,3],[1,3,5],[1,4,4],[2,5,6]], nums = [2,1,2,1,3,1]

Output: [6,2]

Explanation:

In the image below, nodes are colored by their corresponding values in nums

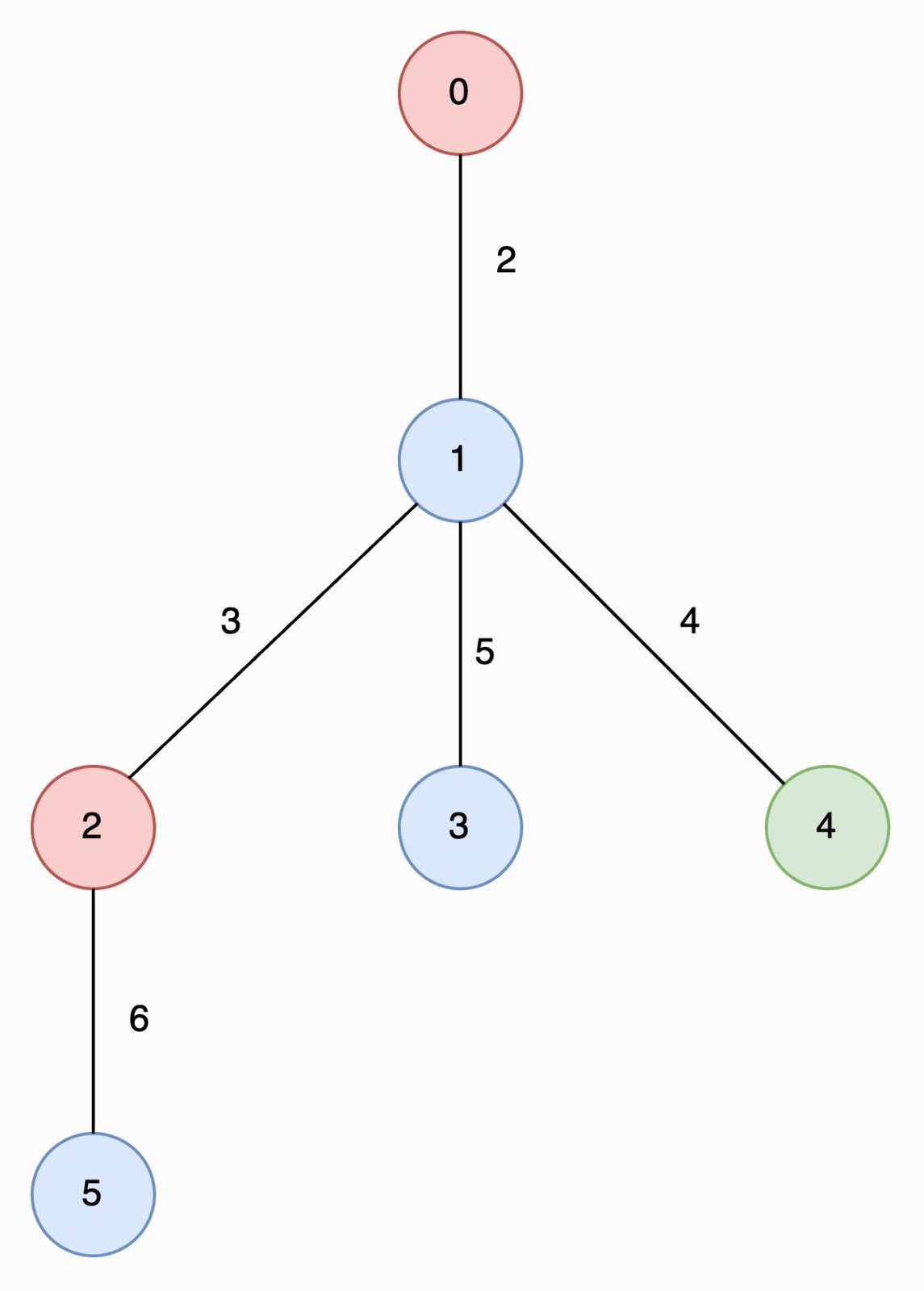
The longest special paths are 2 -> 5 and 0 -> 1 -> 4, both having a length of 6. The minimum number of nodes across all longest special paths is 2.

Example 2:

Input: edges = [[1,0,8]], nums = [2,2]

Output: [0,1]

Explanation:

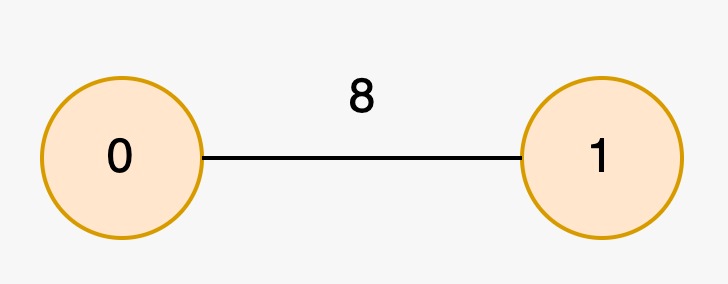
The longest special paths are 0 and 1, both having a length of 0. The minimum number of nodes across all longest special paths is 1.

Constraints:

• 2 <= n <= 5 * 104
• edges.length == n - 1
• edges[i].length == 3
• 0 <= ui, vi < n
• 1 <= lengthi <= 103
• nums.length == n
• 0 <= nums[i] <= 5 * 104
• The input is generated such that edges represents a valid tree.

Solution

class Solution {
    private lateinit var adj: Array<ArrayList<IntArray>>
    private lateinit var nums: IntArray
    private lateinit var dist: IntArray
    private lateinit var lastOccur: IntArray
    private lateinit var pathStack: ArrayList<Int>
    private var minIndex = 0
    private var maxLen = 0
    private var minNodesForMaxLen = 0

    fun longestSpecialPath(edges: Array<IntArray>, nums: IntArray): IntArray {
        val n = nums.size
        this.nums = nums
        adj = Array<ArrayList<IntArray>>(n) { ArrayList<IntArray>() }
        for (i in 0..<n) {
            adj[i] = ArrayList<IntArray>()
        }
        for (e in edges) {
            val u = e[0]
            val v = e[1]
            val w = e[2]
            adj[u].add(intArrayOf(v, w))
            adj[v].add(intArrayOf(u, w))
        }
        dist = IntArray(n)
        buildDist(0, -1, 0)
        var maxVal = 0
        for (`val` in nums) {
            if (`val` > maxVal) {
                maxVal = `val`
            }
        }
        lastOccur = IntArray(maxVal + 1)
        lastOccur.fill(-1)
        pathStack = ArrayList<Int>()
        minIndex = 0
        maxLen = 0
        minNodesForMaxLen = Int.Companion.MAX_VALUE
        dfs(0, -1)
        return intArrayOf(maxLen, minNodesForMaxLen)
    }

    private fun buildDist(u: Int, parent: Int, currDist: Int) {
        dist[u] = currDist
        for (edge in adj[u]) {
            val v = edge[0]
            val w = edge[1]
            if (v == parent) {
                continue
            }
            buildDist(v, u, currDist + w)
        }
    }

    private fun dfs(u: Int, parent: Int) {
        val stackPos = pathStack.size
        pathStack.add(u)
        val `val` = nums[u]
        val oldPos = lastOccur[`val`]
        val oldMinIndex = minIndex
        lastOccur[`val`] = stackPos
        if (oldPos >= minIndex) {
            minIndex = oldPos + 1
        }
        if (minIndex <= stackPos) {
            val ancestor = pathStack[minIndex]
            val pathLength = dist[u] - dist[ancestor]
            val pathNodes = stackPos - minIndex + 1
            if (pathLength > maxLen) {
                maxLen = pathLength
                minNodesForMaxLen = pathNodes
            } else if (pathLength == maxLen && pathNodes < minNodesForMaxLen) {
                minNodesForMaxLen = pathNodes
            }
        }
        for (edge in adj[u]) {
            val v = edge[0]
            if (v == parent) {
                continue
            }
            dfs(v, u)
        }
        pathStack.removeAt(pathStack.size - 1)
        lastOccur[`val`] = oldPos
        minIndex = oldMinIndex
    }
}

This site is open source. Improve this page.