LeetCode in Kotlin

3378. Count Connected Components in LCM Graph

Hard

You are given an array of integers nums of size n and a positive integer threshold.

There is a graph consisting of n nodes with the ith node having a value of nums[i]. Two nodes i and j in the graph are connected via an undirected edge if lcm(nums[i], nums[j]) <= threshold.

Return the number of connected components in this graph.

A connected component is a subgraph of a graph in which there exists a path between any two vertices, and no vertex of the subgraph shares an edge with a vertex outside of the subgraph.

The term lcm(a, b) denotes the least common multiple of a and b.

Example 1:

Input: nums = [2,4,8,3,9], threshold = 5

Output: 4

Explanation:

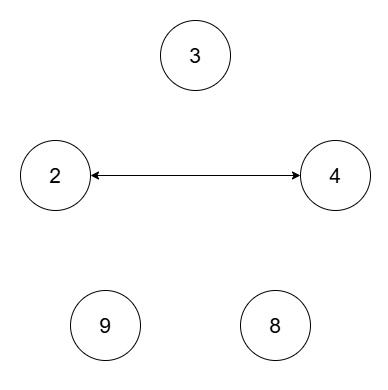
The four connected components are (2, 4), (3), (8), (9).

Example 2:

Input: nums = [2,4,8,3,9,12], threshold = 10

Output: 2

Explanation:

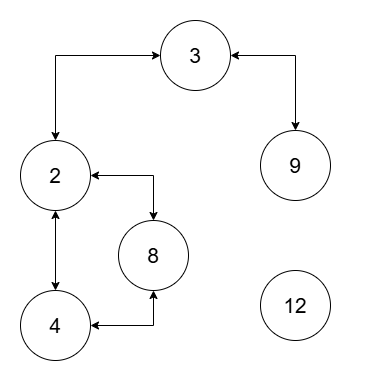
The two connected components are (2, 3, 4, 8, 9), and (12).

Constraints:

• 1 <= nums.length <= 105
• 1 <= nums[i] <= 109
• All elements of nums are unique.
• 1 <= threshold <= 2 * 105

Solution

class Solution {
    private class UnionFind(n: Int) {
        var parent = IntArray(n) { it }
        var rank = IntArray(n)
        var totalComponents = n

        fun find(u: Int): Int {
            if (parent[u] == u) {
                return u
            }
            parent[u] = find(parent[u])
            return parent[u]
        }

        fun union(u: Int, v: Int) {
            val parentU = find(u)
            val parentV = find(v)
            if (parentU != parentV) {
                totalComponents--
                when {
                    rank[parentU] == rank[parentV] -> {
                        parent[parentV] = parentU
                        rank[parentU]++
                    }
                    rank[parentU] > rank[parentV] -> parent[parentV] = parentU
                    else -> parent[parentU] = parentV
                }
            }
        }
    }

    fun countComponents(nums: IntArray, threshold: Int): Int {
        val goodNums = nums.filter { it <= threshold }
        val totalNums = nums.size
        if (goodNums.isEmpty()) {
            return totalNums
        }
        val uf = UnionFind(goodNums.size)
        val presentElements = IntArray(threshold + 1) { -1 }
        goodNums.forEachIndexed { index, num ->
            presentElements[num] = index
        }
        for (d in goodNums) {
            for (i in d..threshold step d) {
                if (presentElements[i] == -1) {
                    presentElements[i] = presentElements[d]
                } else if (presentElements[i] != presentElements[d]) {
                    uf.union(presentElements[i], presentElements[d])
                }
            }
        }
        return uf.totalComponents + totalNums - goodNums.size
    }
}

This site is open source. Improve this page.