LeetCode in Kotlin

3363. Find the Maximum Number of Fruits Collected

Hard

There is a game dungeon comprised of n x n rooms arranged in a grid.

You are given a 2D array fruits of size n x n, where fruits[i][j] represents the number of fruits in the room (i, j). Three children will play in the game dungeon, with initial positions at the corner rooms (0, 0), (0, n - 1), and (n - 1, 0).

The children will make exactly n - 1 moves according to the following rules to reach the room (n - 1, n - 1):

• The child starting from (0, 0) must move from their current room (i, j) to one of the rooms (i + 1, j + 1), (i + 1, j), and (i, j + 1) if the target room exists.
• The child starting from (0, n - 1) must move from their current room (i, j) to one of the rooms (i + 1, j - 1), (i + 1, j), and (i + 1, j + 1) if the target room exists.
• The child starting from (n - 1, 0) must move from their current room (i, j) to one of the rooms (i - 1, j + 1), (i, j + 1), and (i + 1, j + 1) if the target room exists.

When a child enters a room, they will collect all the fruits there. If two or more children enter the same room, only one child will collect the fruits, and the room will be emptied after they leave.

Return the maximum number of fruits the children can collect from the dungeon.

Example 1:

Input: fruits = [[1,2,3,4],[5,6,8,7],[9,10,11,12],[13,14,15,16]]

Output: 100

Explanation:

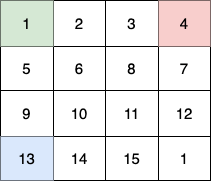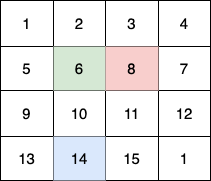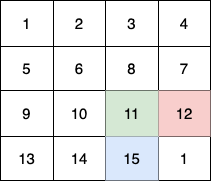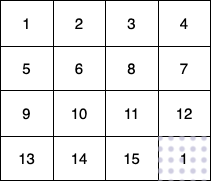
In this example:

• The 1^st child (green) moves on the path (0,0) -> (1,1) -> (2,2) -> (3, 3).
• The 2^nd child (red) moves on the path (0,3) -> (1,2) -> (2,3) -> (3, 3).
• The 3^rd child (blue) moves on the path (3,0) -> (3,1) -> (3,2) -> (3, 3).

In total they collect 1 + 6 + 11 + 1 + 4 + 8 + 12 + 13 + 14 + 15 = 100 fruits.

Example 2:

Input: fruits = [[1,1],[1,1]]

Output: 4

Explanation:

In this example:

• The 1^st child moves on the path (0,0) -> (1,1).
• The 2^nd child moves on the path (0,1) -> (1,1).
• The 3^rd child moves on the path (1,0) -> (1,1).

In total they collect 1 + 1 + 1 + 1 = 4 fruits.

Constraints:

• 2 <= n == fruits.length == fruits[i].length <= 1000
• 0 <= fruits[i][j] <= 1000

Solution

import kotlin.math.max

class Solution {
    fun maxCollectedFruits(fruits: Array<IntArray>): Int {
        val n = fruits.size
        // Set inaccessible cells to 0
        for (i in 0..<n) {
            for (j in 0..<n) {
                if (i < j && j < n - 1 - i) {
                    fruits[i][j] = 0
                }
                if (j < i && i < n - 1 - j) {
                    fruits[i][j] = 0
                }
            }
        }
        var res = 0
        for (i in 0..<n) {
            res += fruits[i][i]
        }
        for (i in 1..<n) {
            for (j in i + 1..<n) {
                fruits[i][j] = (
                    fruits[i][j] + max(
                        fruits[i - 1][j - 1],
                        max(fruits[i - 1][j], if (j + 1 < n) fruits[i - 1][j + 1] else 0),
                    )
                    )
            }
        }
        for (j in 1..<n) {
            for (i in j + 1..<n) {
                fruits[i][j] = (
                    fruits[i][j] + max(
                        fruits[i - 1][j - 1],
                        max(fruits[i][j - 1], if (i + 1 < n) fruits[i + 1][j - 1] else 0),
                    )
                    )
            }
        }
        return res + fruits[n - 1][n - 2] + fruits[n - 2][n - 1]
    }
}

This site is open source. Improve this page.