LeetCode in Kotlin

3331. Find Subtree Sizes After Changes

Medium

You are given a tree rooted at node 0 that consists of n nodes numbered from 0 to n - 1. The tree is represented by an array parent of size n, where parent[i] is the parent of node i. Since node 0 is the root, parent[0] == -1.

You are also given a string s of length n, where s[i] is the character assigned to node i.

We make the following changes on the tree one time simultaneously for all nodes x from 1 to n - 1:

• Find the closest node y to node x such that y is an ancestor of x, and s[x] == s[y].
• If node y does not exist, do nothing.
• Otherwise, remove the edge between x and its current parent and make node y the new parent of x by adding an edge between them.

Return an array answer of size n where answer[i] is the size of the subtree rooted at node i in the final tree.

A subtree of treeName is a tree consisting of a node in treeName and all of its descendants.

Example 1:

Input: parent = [-1,0,0,1,1,1], s = “abaabc”

Output: [6,3,1,1,1,1]

Explanation:

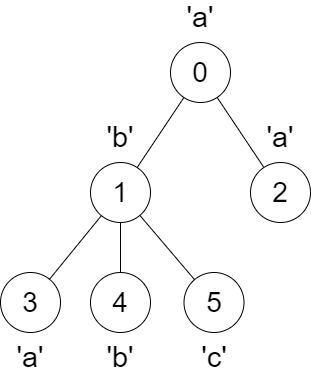
The parent of node 3 will change from node 1 to node 0.

Example 2:

Input: parent = [-1,0,4,0,1], s = “abbba”

Output: [5,2,1,1,1]

Explanation:

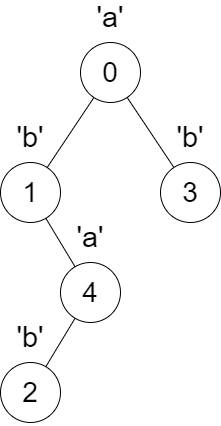
The following changes will happen at the same time:

• The parent of node 4 will change from node 1 to node 0.
• The parent of node 2 will change from node 4 to node 1.

Constraints:

• n == parent.length == s.length
• 1 <= n <= 105
• 0 <= parent[i] <= n - 1 for all i >= 1.
• parent[0] == -1
• parent represents a valid tree.
• s consists only of lowercase English letters.

Solution

class Solution {
    private lateinit var finalAns: IntArray

    fun findSubtreeSizes(parent: IntArray, s: String): IntArray {
        val n = parent.size
        val arr = s.toCharArray()
        val newParent = IntArray(n)
        finalAns = IntArray(n)
        val tree = HashMap<Int, ArrayList<Int>>()

        for (i in 1 until n) {
            var parentNode = parent[i]
            newParent[i] = parentNode
            while (parentNode != -1) {
                if (arr[parentNode] == arr[i]) {
                    newParent[i] = parentNode
                    break
                }
                parentNode = parent[parentNode]
            }
        }

        for (i in 1 until n) {
            if (!tree.containsKey(newParent[i])) {
                tree.put(newParent[i], ArrayList<Int>())
            }

            tree[newParent[i]]!!.add(i)
        }

        findNodes(0, tree)
        return finalAns
    }

    private fun findNodes(parent: Int, tree: HashMap<Int, ArrayList<Int>>): Int {
        var count = 1
        if (tree.containsKey(parent)) {
            for (i in tree[parent]!!) {
                count += findNodes(i, tree)
            }
        }
        finalAns[parent] = count
        return count
    }
}

This site is open source. Improve this page.