LeetCode in Kotlin
3257. Maximum Value Sum by Placing Three Rooks II
Hard
You are given a m x n 2D array board representing a chessboard, where board[i][j] represents the value of the cell (i, j).
Rooks in the same row or column attack each other. You need to place three rooks on the chessboard such that the rooks do not attack each other.
Return the maximum sum of the cell values on which the rooks are placed.
Example 1:
Input: board = [[-3,1,1,1],[-3,1,-3,1],[-3,2,1,1]]
Output: 4
Explanation:
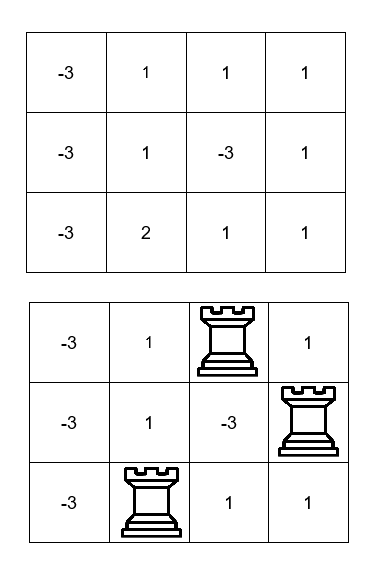
We can place the rooks in the cells (0, 2), (1, 3), and (2, 1) for a sum of 1 + 1 + 2 = 4.
Example 2:
Input: board = [[1,2,3],[4,5,6],[7,8,9]]
Output: 15
Explanation:
We can place the rooks in the cells (0, 0), (1, 1), and (2, 2) for a sum of 1 + 5 + 9 = 15.
Example 3:
Input: board = [[1,1,1],[1,1,1],[1,1,1]]
Output: 3
Explanation:
We can place the rooks in the cells (0, 2), (1, 1), and (2, 0) for a sum of 1 + 1 + 1 = 3.
Constraints:
3 <= m == board.length <= 5003 <= n == board[i].length <= 500-109 <= board[i][j] <= 109
Solution
import kotlin.math.max
class Solution {
fun maximumValueSum(board: Array<IntArray>): Long {
val n = board.size
val m = board[0].size
val tb = Array(n) { IntArray(m) }
tb[0] = board[0].copyOf(m)
for (i in 1 until n) {
for (j in 0 until m) {
tb[i][j] = max(tb[i - 1][j], board[i][j])
}
}
val bt = Array(n) { IntArray(m) }
bt[n - 1] = board[n - 1].copyOf(m)
for (i in n - 2 downTo 0) {
for (j in 0 until m) {
bt[i][j] = max(bt[i + 1][j], board[i][j])
}
}
var ans = Long.MIN_VALUE
for (i in 1 until n - 1) {
val max3Top = getMax3(tb[i - 1])
val max3Cur = getMax3(board[i])
val max3Bottom = getMax3(bt[i + 1])
for (topCand in max3Top) {
for (curCand in max3Cur) {
for (bottomCand in max3Bottom) {
if (topCand[1] != curCand[1] && topCand[1] != bottomCand[1] && curCand[1] != bottomCand[1]) {
val cand = topCand[0].toLong() + curCand[0] + bottomCand[0]
ans = max(ans, cand)
}
}
}
}
}
return ans
}
private fun getMax3(row: IntArray): Array<IntArray> {
val m = row.size
val ans = Array(3) { IntArray(2) }
ans.fill(intArrayOf(Int.MIN_VALUE, -1))
for (j in 0 until m) {
if (row[j] >= ans[0][0]) {
ans[2] = ans[1]
ans[1] = ans[0]
ans[0] = intArrayOf(row[j], j)
} else if (row[j] >= ans[1][0]) {
ans[2] = ans[1]
ans[1] = intArrayOf(row[j], j)
} else if (row[j] > ans[2][0]) {
ans[2] = intArrayOf(row[j], j)
}
}
return ans
}
}

