LeetCode in Kotlin

3241. Time Taken to Mark All Nodes

Hard

There exists an undirected tree with n nodes numbered 0 to n - 1. You are given a 2D integer array edges of length n - 1, where edges[i] = [ui, vi] indicates that there is an edge between nodes ui and vi in the tree.

Initially, all nodes are unmarked. For each node i:

• If i is odd, the node will get marked at time x if there is at least one node adjacent to it which was marked at time x - 1.
• If i is even, the node will get marked at time x if there is at least one node adjacent to it which was marked at time x - 2.

Return an array times where times[i] is the time when all nodes get marked in the tree, if you mark node i at time t = 0.

Note that the answer for each times[i] is independent, i.e. when you mark node i all other nodes are unmarked.

Example 1:

Input: edges = [[0,1],[0,2]]

Output: [2,4,3]

Explanation:

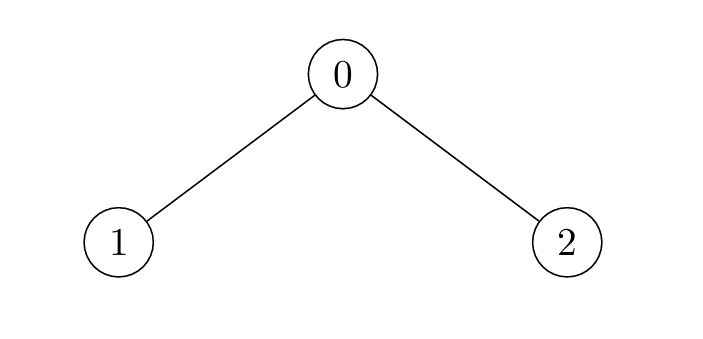
• For i = 0:
  • Node 1 is marked at t = 1, and Node 2 at t = 2.
• For i = 1:
  • Node 0 is marked at t = 2, and Node 2 at t = 4.
• For i = 2:
  • Node 0 is marked at t = 2, and Node 1 at t = 3.

Example 2:

Input: edges = [[0,1]]

Output: [1,2]

Explanation:

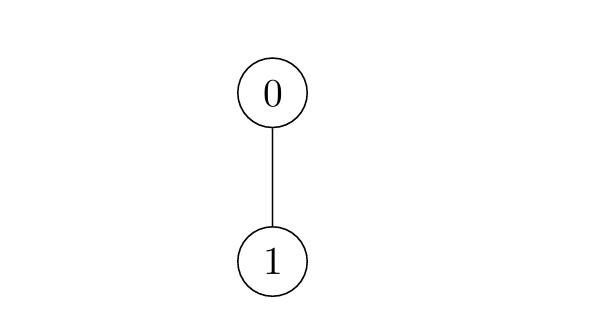
• For i = 0:
  • Node 1 is marked at t = 1.
• For i = 1:
  • Node 0 is marked at t = 2.

Example 3:

Input: edges = [[2,4],[0,1],[2,3],[0,2]]

Output: [4,6,3,5,5]

Explanation:

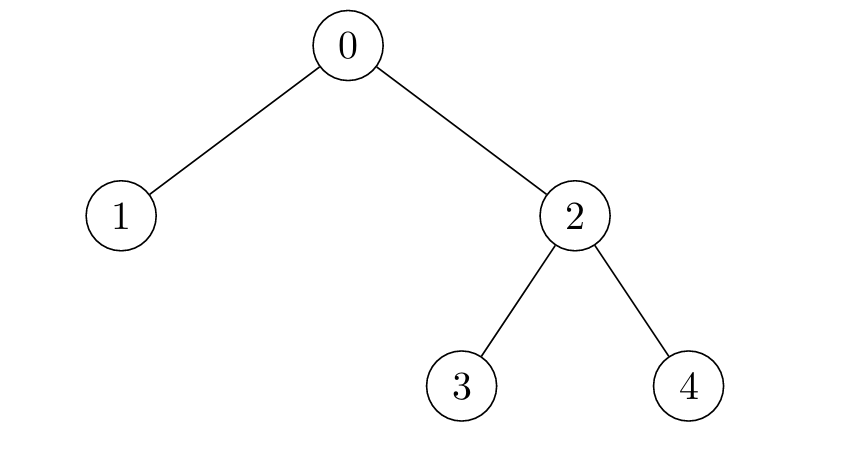
Constraints:

• 2 <= n <= 105
• edges.length == n - 1
• edges[i].length == 2
• 0 <= edges[i][0], edges[i][1] <= n - 1
• The input is generated such that edges represents a valid tree.

Solution

import kotlin.math.max

class Solution {
    private lateinit var head: IntArray
    private lateinit var nxt: IntArray
    private lateinit var to: IntArray
    private lateinit var last: IntArray
    private lateinit var lastNo: IntArray
    private lateinit var second: IntArray
    private lateinit var ans: IntArray

    fun timeTaken(edges: Array<IntArray>): IntArray {
        val n = edges.size + 1
        head = IntArray(n)
        nxt = IntArray(n shl 1)
        to = IntArray(n shl 1)
        head.fill(-1)
        var i = 0
        var j = 2
        while (i < edges.size) {
            val u = edges[i][0]
            val v = edges[i][1]
            nxt[j] = head[u]
            head[u] = j
            to[j] = v
            j++
            nxt[j] = head[v]
            head[v] = j
            to[j] = u
            j++
            i++
        }
        last = IntArray(n)
        lastNo = IntArray(n)
        second = IntArray(n)
        ans = IntArray(n)
        dfs(-1, 0)
        System.arraycopy(last, 0, ans, 0, n)
        dfs2(-1, 0, 0)
        return ans
    }

    private fun dfs2(f: Int, u: Int, preLast: Int) {
        var e = head[u]
        var v: Int
        while (e != -1) {
            v = to[e]
            if (f != v) {
                val pl = if (v == lastNo[u]) {
                    (
                        max(
                            preLast,
                            second[u],
                        ) + (if ((u and 1) == 0) 2 else 1)
                        )
                } else {
                    (
                        max(
                            preLast,
                            last[u],
                        ) + (if ((u and 1) == 0) 2 else 1)
                        )
                }
                ans[v] = max(ans[v], pl)
                dfs2(u, v, pl)
            }
            e = nxt[e]
        }
    }

    private fun dfs(f: Int, u: Int) {
        var e = head[u]
        var v: Int
        while (e != -1) {
            v = to[e]
            if (f != v) {
                dfs(u, v)
                val t = last[v] + (if ((v and 1) == 0) 2 else 1)
                if (last[u] < t) {
                    second[u] = last[u]
                    last[u] = t
                    lastNo[u] = v
                } else if (second[u] < t) {
                    second[u] = t
                }
            }
            e = nxt[e]
        }
    }
}

This site is open source. Improve this page.