LeetCode in Kotlin
3225. Maximum Score From Grid Operations
Hard
You are given a 2D matrix grid of size n x n. Initially, all cells of the grid are colored white. In one operation, you can select any cell of indices (i, j), and color black all the cells of the jth column starting from the top row down to the ith row.
The grid score is the sum of all grid[i][j] such that cell (i, j) is white and it has a horizontally adjacent black cell.
Return the maximum score that can be achieved after some number of operations.
Example 1:
Input: grid = [[0,0,0,0,0],[0,0,3,0,0],[0,1,0,0,0],[5,0,0,3,0],[0,0,0,0,2]]
Output: 11
Explanation:
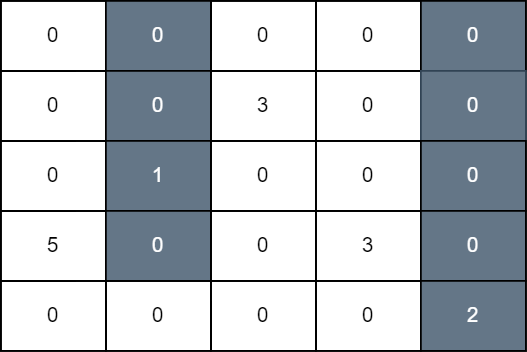
In the first operation, we color all cells in column 1 down to row 3, and in the second operation, we color all cells in column 4 down to the last row. The score of the resulting grid is grid[3][0] + grid[1][2] + grid[3][3] which is equal to 11.
Example 2:
Input: grid = [[10,9,0,0,15],[7,1,0,8,0],[5,20,0,11,0],[0,0,0,1,2],[8,12,1,10,3]]
Output: 94
Explanation:
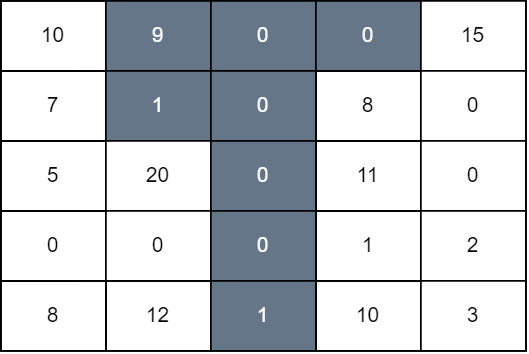
We perform operations on 1, 2, and 3 down to rows 1, 4, and 0, respectively. The score of the resulting grid is grid[0][0] + grid[1][0] + grid[2][1] + grid[4][1] + grid[1][3] + grid[2][3] + grid[3][3] + grid[4][3] + grid[0][4] which is equal to 94.
Constraints:
1 <= n == grid.length <= 100n == grid[i].length0 <= grid[i][j] <= 109
Solution
import kotlin.math.max
class Solution {
fun maximumScore(grid: Array<IntArray>): Long {
val n = grid.size
var dp1 = LongArray(n)
var dp2 = LongArray(n + 1)
var dp3 = LongArray(n + 1)
var dp12 = LongArray(n)
var dp22 = LongArray(n + 1)
var dp32 = LongArray(n + 1)
var res: Long = 0
for (i in 0 until n) {
var sum: Long = 0
var pre: Long = 0
for (ints in grid) {
sum += ints[i].toLong()
}
for (j in n - 1 downTo 0) {
var s2 = sum
dp12[j] = s2 + dp3[n]
for (k in 0..j) {
s2 -= grid[k][i].toLong()
var v = max((dp1[k] + s2), (dp3[j] + s2))
v = max(v, (pre + s2))
dp12[j] = max(dp12[j], v)
if (k == j) {
dp32[j] = v
dp22[j] = dp32[j]
res = max(res, v)
}
}
if (i > 0) {
pre = max((pre + grid[j][i]), (dp2[j] + grid[j][i]))
}
sum -= grid[j][i].toLong()
}
dp32[n] = pre
dp22[n] = dp32[n]
res = max(res, pre)
for (j in 1..n) {
dp32[j] = max(dp32[j], dp32[j - 1])
}
var tem = dp1
dp1 = dp12
dp12 = tem
tem = dp2
dp2 = dp22
dp22 = tem
tem = dp3
dp3 = dp32
dp32 = tem
}
return res
}
}

