LeetCode in Kotlin

3219. Minimum Cost for Cutting Cake II

Hard

There is an m x n cake that needs to be cut into 1 x 1 pieces.

You are given integers m, n, and two arrays:

• horizontalCut of size m - 1, where horizontalCut[i] represents the cost to cut along the horizontal line i.
• verticalCut of size n - 1, where verticalCut[j] represents the cost to cut along the vertical line j.

In one operation, you can choose any piece of cake that is not yet a 1 x 1 square and perform one of the following cuts:

1. Cut along a horizontal line i at a cost of horizontalCut[i].
2. Cut along a vertical line j at a cost of verticalCut[j].

After the cut, the piece of cake is divided into two distinct pieces.

The cost of a cut depends only on the initial cost of the line and does not change.

Return the minimum total cost to cut the entire cake into 1 x 1 pieces.

Example 1:

Input: m = 3, n = 2, horizontalCut = [1,3], verticalCut = [5]

Output: 13

Explanation:

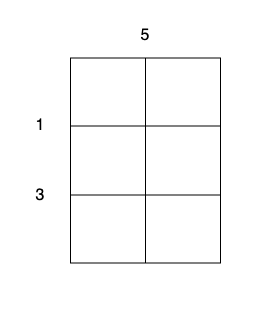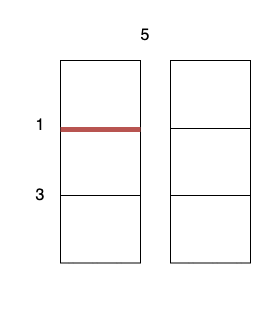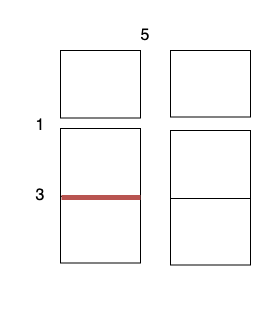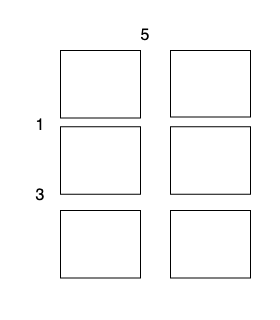
• Perform a cut on the vertical line 0 with cost 5, current total cost is 5.
• Perform a cut on the horizontal line 0 on 3 x 1 subgrid with cost 1.
• Perform a cut on the horizontal line 0 on 3 x 1 subgrid with cost 1.
• Perform a cut on the horizontal line 1 on 2 x 1 subgrid with cost 3.
• Perform a cut on the horizontal line 1 on 2 x 1 subgrid with cost 3.

The total cost is 5 + 1 + 1 + 3 + 3 = 13.

Example 2:

Input: m = 2, n = 2, horizontalCut = [7], verticalCut = [4]

Output: 15

Explanation:

• Perform a cut on the horizontal line 0 with cost 7.
• Perform a cut on the vertical line 0 on 1 x 2 subgrid with cost 4.
• Perform a cut on the vertical line 0 on 1 x 2 subgrid with cost 4.

The total cost is 7 + 4 + 4 = 15.

Constraints:

• 1 <= m, n <= 105
• horizontalCut.length == m - 1
• verticalCut.length == n - 1
• 1 <= horizontalCut[i], verticalCut[i] <= 103

Solution

class Solution {
    fun minimumCost(m: Int, n: Int, horizontalCut: IntArray, verticalCut: IntArray): Long {
        val horizontalCounts = IntArray(N)
        val verticalCounts = IntArray(N)
        var max = 0
        for (x in horizontalCut) {
            if (x > max) {
                max = x
            }
            horizontalCounts[x]++
        }
        for (x in verticalCut) {
            if (x > max) {
                max = x
            }
            verticalCounts[x]++
        }
        var ans: Long = 0
        var horizontalCount = 1
        var verticalCount = 1
        for (x in max downTo 1) {
            ans += horizontalCounts[x].toLong() * x * horizontalCount
            verticalCount += horizontalCounts[x]
            horizontalCounts[x] = 0
            ans += verticalCounts[x].toLong() * x * verticalCount
            horizontalCount += verticalCounts[x]
            verticalCounts[x] = 0
        }
        return ans
    }

    companion object {
        private const val N = 1001
    }
}

This site is open source. Improve this page.