LeetCode in Kotlin

3161. Block Placement Queries

Hard

There exists an infinite number line, with its origin at 0 and extending towards the positive x-axis.

You are given a 2D array queries, which contains two types of queries:

1. For a query of type 1, queries[i] = [1, x]. Build an obstacle at distance x from the origin. It is guaranteed that there is no obstacle at distance x when the query is asked.
2. For a query of type 2, queries[i] = [2, x, sz]. Check if it is possible to place a block of size sz anywhere in the range [0, x] on the line, such that the block entirely lies in the range [0, x]. A block cannot be placed if it intersects with any obstacle, but it may touch it. Note that you do not actually place the block. Queries are separate.

Return a boolean array results, where results[i] is true if you can place the block specified in the ith query of type 2, and false otherwise.

Example 1:

Input: queries = [[1,2],[2,3,3],[2,3,1],[2,2,2]]

Output: [false,true,true]

Explanation:

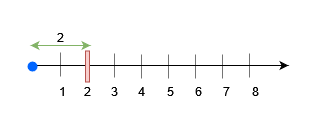
For query 0, place an obstacle at x = 2. A block of size at most 2 can be placed before x = 3.

Example 2:

Input: queries = [[1,7],[2,7,6],[1,2],[2,7,5],[2,7,6]]

Output: [true,true,false]

Explanation:

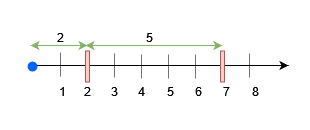
• Place an obstacle at x = 7 for query 0. A block of size at most 7 can be placed before x = 7.
• Place an obstacle at x = 2 for query 2. Now, a block of size at most 5 can be placed before x = 7, and a block of size at most 2 before x = 2.

Constraints:

• 1 <= queries.length <= 15 * 104
• 2 <= queries[i].length <= 3
• 1 <= queries[i][0] <= 2
• 1 <= x, sz <= min(5 * 104, 3 * queries.length)
• The input is generated such that for queries of type 1, no obstacle exists at distance x when the query is asked.
• The input is generated such that there is at least one query of type 2.

Solution

import kotlin.math.max

class Solution {
    fun getResults(queries: Array<IntArray>): List<Boolean> {
        val m = queries.size
        val pos = IntArray(m + 1)
        var size = 0
        pos[size++] = 0
        var max = 0
        for (q in queries) {
            max = max(max.toDouble(), q[1].toDouble()).toInt()
            if (q[0] == 1) {
                pos[size++] = q[1]
            }
        }
        pos.sort(0, size)
        max++
        val left = UnionFind(max + 1)
        val right = UnionFind(max + 1)
        val bit = BIT(max)
        initializePositions(size, pos, bit, left, right, max)
        return listOf<Boolean>(*getBooleans(queries, m, size, left, right, bit))
    }

    private fun initializePositions(
        size: Int,
        pos: IntArray,
        bit: BIT,
        left: UnionFind,
        right: UnionFind,
        max: Int,
    ) {
        for (i in 1..<size) {
            val pre = pos[i - 1]
            val cur = pos[i]
            bit.update(cur, cur - pre)
            for (j in pre + 1..<cur) {
                left.parent[j] = pre
                right.parent[j] = cur
            }
        }
        for (j in pos[size - 1] + 1..<max) {
            left.parent[j] = pos[size - 1]
            right.parent[j] = max
        }
    }

    private fun getBooleans(
        queries: Array<IntArray>,
        m: Int,
        size: Int,
        left: UnionFind,
        right: UnionFind,
        bit: BIT,
    ): Array<Boolean> {
        val ans = Array<Boolean>(m - size + 1) { false }
        var index = ans.size - 1
        for (i in m - 1 downTo 0) {
            val q = queries[i]
            val x = q[1]
            val pre = left.find(x - 1)
            if (q[0] == 1) {
                val next = right.find(x + 1)
                left.parent[x] = pre
                right.parent[x] = next
                bit.update(next, next - pre)
            } else {
                val maxGap = max(bit.query(pre), x - pre)
                ans[index--] = maxGap >= q[2]
            }
        }
        return ans
    }

    private class BIT(var n: Int) {
        var tree: IntArray = IntArray(n)

        fun update(i: Int, v: Int) {
            var i = i
            while (i < n) {
                tree[i] = max(tree[i], v)
                i += i and -i
            }
        }

        fun query(i: Int): Int {
            var i = i
            var result = 0
            while (i > 0) {
                result = max(result, tree[i])
                i = i and i - 1
            }
            return result
        }
    }

    private class UnionFind(n: Int) {
        val parent: IntArray = IntArray(n)

        init {
            for (i in 1..<n) {
                parent[i] = i
            }
        }

        fun find(x: Int): Int {
            if (parent[x] != x) {
                parent[x] = find(parent[x])
            }
            return parent[x]
        }
    }
}

This site is open source. Improve this page.