LeetCode in Kotlin

3123. Find Edges in Shortest Paths

Hard

You are given an undirected weighted graph of n nodes numbered from 0 to n - 1. The graph consists of m edges represented by a 2D array edges, where edges[i] = [a_i, b_i, w_i] indicates that there is an edge between nodes a_i and b_i with weight w_i.

Consider all the shortest paths from node 0 to node n - 1 in the graph. You need to find a boolean array answer where answer[i] is true if the edge edges[i] is part of at least one shortest path. Otherwise, answer[i] is false.

Return the array answer.

Note that the graph may not be connected.

Example 1:

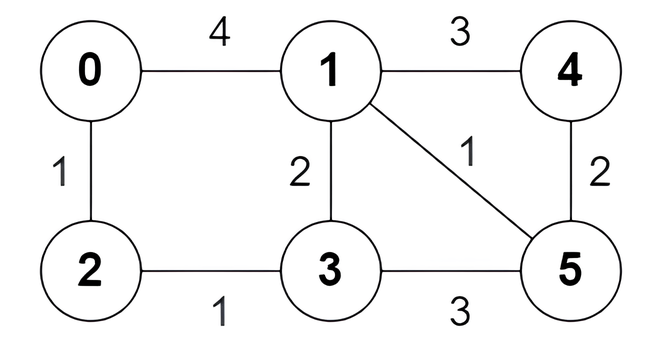
Input: n = 6, edges = [[0,1,4],[0,2,1],[1,3,2],[1,4,3],[1,5,1],[2,3,1],[3,5,3],[4,5,2]]

Output: [true,true,true,false,true,true,true,false]

Explanation:

The following are all the shortest paths between nodes 0 and 5:

The path 0 -> 1 -> 5: The sum of weights is 4 + 1 = 5.
The path 0 -> 2 -> 3 -> 5: The sum of weights is 1 + 1 + 3 = 5.
The path 0 -> 2 -> 3 -> 1 -> 5: The sum of weights is 1 + 1 + 2 + 1 = 5.

Example 2:

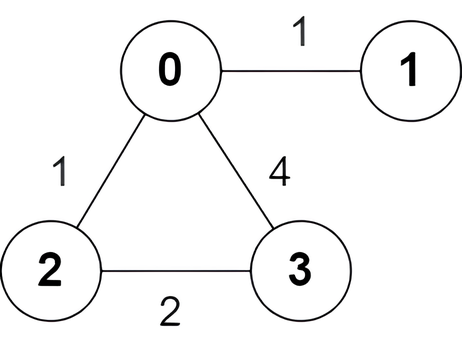
Input: n = 4, edges = [[2,0,1],[0,1,1],[0,3,4],[3,2,2]]

Output: [true,false,false,true]

Explanation:

There is one shortest path between nodes 0 and 3, which is the path 0 -> 2 -> 3 with the sum of weights 1 + 2 = 3.

Constraints:

2 <= n <= 5 * 10⁴
m == edges.length
1 <= m <= min(5 * 10⁴, n * (n - 1) / 2)
0 <= a_i, b_i < n
a_i != b_i
1 <= w_i <= 10⁵
There are no repeated edges.

Solution

import java.util.PriorityQueue

class Solution {
    private lateinit var edge: IntArray
    private lateinit var weight: IntArray
    private lateinit var next: IntArray
    private lateinit var head: IntArray
    private var index = 0

    private fun add(u: Int, v: Int, w: Int) {
        edge[index] = v
        weight[index] = w
        next[index] = head[u]
        head[u] = index++
    }

    fun findAnswer(n: Int, edges: Array<IntArray>): BooleanArray {
        val m = edges.size
        edge = IntArray(m shl 1)
        weight = IntArray(m shl 1)
        next = IntArray(m shl 1)
        head = IntArray(n)
        for (i in 0 until n) {
            head[i] = -1
        }
        index = 0
        for (localEdge in edges) {
            val u = localEdge[0]
            val v = localEdge[1]
            val w = localEdge[2]
            add(u, v, w)
            add(v, u, w)
        }
        val pq = PriorityQueue { a: LongArray, b: LongArray -> if (a[1] < b[1]) -1 else 1 }
        val distances = LongArray(n)
        distances.fill(1e12.toLong())
        pq.offer(longArrayOf(0, 0))
        distances[0] = 0
        while (pq.isNotEmpty()) {
            val cur = pq.poll()
            val u = cur[0].toInt()
            val distance = cur[1]
            if (distance > distances[u]) {
                continue
            }
            if (u == n - 1) {
                break
            }
            var localIndex = head[u]
            while (localIndex != -1) {
                val v = edge[localIndex]
                val w = weight[localIndex]
                val newDistance = distance + w
                if (newDistance < distances[v]) {
                    distances[v] = newDistance
                    pq.offer(longArrayOf(v.toLong(), newDistance))
                }
                localIndex = next[localIndex]
            }
        }
        val ans = BooleanArray(m)
        if (distances[n - 1] >= 1e12.toLong()) {
            return ans
        }
        dfs(distances, n - 1, -1, ans)
        return ans
    }

    private fun dfs(distances: LongArray, u: Int, pre: Int, ans: BooleanArray) {
        var localIndex = head[u]
        while (localIndex != -1) {
            val v = edge[localIndex]
            val w = weight[localIndex]
            val i = localIndex shr 1
            if (distances[v] + w != distances[u]) {
                localIndex = next[localIndex]
                continue
            }
            ans[i] = true
            if (v == pre) {
                localIndex = next[localIndex]
                continue
            }
            dfs(distances, v, u, ans)
            localIndex = next[localIndex]
        }
    }
}

This site is open source. Improve this page.