LeetCode in Kotlin
3122. Minimum Number of Operations to Satisfy Conditions
Medium
You are given a 2D matrix grid of size m x n. In one operation, you can change the value of any cell to any non-negative number. You need to perform some operations such that each cell grid[i][j] is:
- Equal to the cell below it, i.e.
grid[i][j] == grid[i + 1][j](if it exists). - Different from the cell to its right, i.e.
grid[i][j] != grid[i][j + 1](if it exists).
Return the minimum number of operations needed.
Example 1:
Input: grid = [[1,0,2],[1,0,2]]
Output: 0
Explanation:
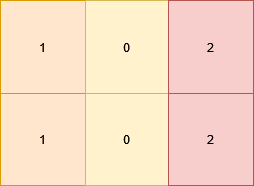
All the cells in the matrix already satisfy the properties.
Example 2:
Input: grid = [[1,1,1],[0,0,0]]
Output: 3
Explanation:
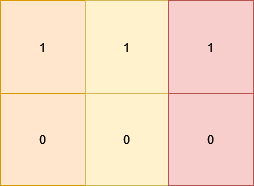
The matrix becomes [[1,0,1],[1,0,1]] which satisfies the properties, by doing these 3 operations:
- Change
grid[1][0]to 1. - Change
grid[0][1]to 0. - Change
grid[1][2]to 1.
Example 3:
Input: grid = [[1],[2],[3]]
Output: 2
Explanation:

There is a single column. We can change the value to 1 in each cell using 2 operations.
Constraints:
1 <= n, m <= 10000 <= grid[i][j] <= 9
Solution
import kotlin.math.min
class Solution {
fun minimumOperations(grid: Array<IntArray>): Int {
val n = grid.size
val m = grid[0].size
val dp = Array(m) { IntArray(10) }
val cnt = Array(m) { IntArray(10) }
for (i in 0 until n) {
for (j in 0 until m) {
cnt[j][grid[i][j]]++
}
}
var first = Int.MAX_VALUE
var second = Int.MAX_VALUE
var firstId = -1
var secondId = -1
for (i in 0..9) {
dp[0][i] = n - cnt[0][i]
if (dp[0][i] <= first) {
second = first
first = dp[0][i]
secondId = firstId
firstId = i
} else if (dp[0][i] < second) {
second = dp[0][i]
secondId = i
}
}
for (j in 1 until m) {
val lastFirstId = firstId
val lastSecondId = secondId
second = Int.MAX_VALUE
first = second
secondId = -1
firstId = secondId
for (i in 0..9) {
var tmp: Int
val fix = n - cnt[j][i]
tmp = if (i == lastFirstId) {
fix + dp[j - 1][lastSecondId]
} else {
fix + dp[j - 1][lastFirstId]
}
if (tmp <= first) {
second = first
first = tmp
secondId = firstId
firstId = i
} else if (tmp < second) {
second = tmp
secondId = i
}
dp[j][i] = tmp
}
}
var ans = Int.MAX_VALUE
for (i in 0..9) {
ans = min(ans, dp[m - 1][i])
}
return ans
}
}

