LeetCode in Kotlin

2876. Count Visited Nodes in a Directed Graph

Hard

There is a directed graph consisting of n nodes numbered from 0 to n - 1 and n directed edges.

You are given a 0-indexed array edges where edges[i] indicates that there is an edge from node i to node edges[i].

Consider the following process on the graph:

• You start from a node x and keep visiting other nodes through edges until you reach a node that you have already visited before on this same process.

Return an array answer where answer[i] is the number of different nodes that you will visit if you perform the process starting from node i.

Example 1:

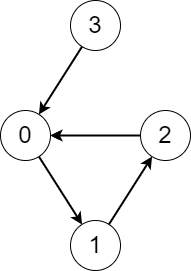
Input: edges = [1,2,0,0]

Output: [3,3,3,4]

Explanation: We perform the process starting from each node in the following way:

• Starting from node 0, we visit the nodes 0 -> 1 -> 2 -> 0. The number of different nodes we visit is 3.
• Starting from node 1, we visit the nodes 1 -> 2 -> 0 -> 1. The number of different nodes we visit is 3.
• Starting from node 2, we visit the nodes 2 -> 0 -> 1 -> 2. The number of different nodes we visit is 3.
• Starting from node 3, we visit the nodes 3 -> 0 -> 1 -> 2 -> 0. The number of different nodes we visit is 4.

Example 2:

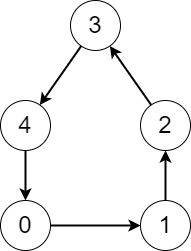
Input: edges = [1,2,3,4,0]

Output: [5,5,5,5,5]

Explanation: Starting from any node we can visit every node in the graph in the process.

Constraints:

• n == edges.length
• 2 <= n <= 105
• 0 <= edges[i] <= n - 1
• edges[i] != i

Solution

class Solution {
    fun countVisitedNodes(edges: List<Int>): IntArray {
        val n = edges.size
        val visited = BooleanArray(n)
        val ans = IntArray(n)
        val level = IntArray(n)
        for (i in 0 until n) {
            if (!visited[i]) {
                visit(edges, 0, i, ans, visited, level)
            }
        }
        return ans
    }

    private fun visit(
        edges: List<Int>,
        count: Int,
        curr: Int,
        ans: IntArray,
        visited: BooleanArray,
        level: IntArray
    ): IntArray {
        if (ans[curr] != 0) {
            return intArrayOf(-1, ans[curr])
        }
        if (visited[curr]) {
            return intArrayOf(level[curr], count - level[curr])
        }
        level[curr] = count
        visited[curr] = true
        val ret = visit(edges, count + 1, edges[curr], ans, visited, level)
        if (ret[0] == -1 || count < ret[0]) {
            ret[1]++
        }
        ans[curr] = ret[1]
        return ret
    }
}

This site is open source. Improve this page.