LeetCode in Kotlin

2858. Minimum Edge Reversals So Every Node Is Reachable

Hard

There is a simple directed graph with n nodes labeled from 0 to n - 1. The graph would form a tree if its edges were bi-directional.

You are given an integer n and a 2D integer array edges, where edges[i] = [ui, vi] represents a directed edge going from node ui to node vi.

An edge reversal changes the direction of an edge, i.e., a directed edge going from node ui to node vi becomes a directed edge going from node vi to node ui.

For every node i in the range [0, n - 1], your task is to independently calculate the minimum number of edge reversals required so it is possible to reach any other node starting from node i through a sequence of directed edges.

Return an integer array answer, where answer[i] is the minimum number of edge reversals required so it is possible to reach any other node starting from node i through a sequence of directed edges.

Example 1:

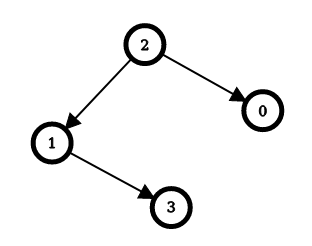
Input: n = 4, edges = [[2,0],[2,1],[1,3]]

Output: [1,1,0,2]

Explanation: The image above shows the graph formed by the edges.

For node 0: after reversing the edge [2,0], it is possible to reach any other node starting from node 0.

So, answer[0] = 1.

For node 1: after reversing the edge [2,1], it is possible to reach any other node starting from node 1.

So, answer[1] = 1.

For node 2: it is already possible to reach any other node starting from node 2.

So, answer[2] = 0.

For node 3: after reversing the edges [1,3] and [2,1], it is possible to reach any other node starting from node 3.

So, answer[3] = 2.

Example 2:

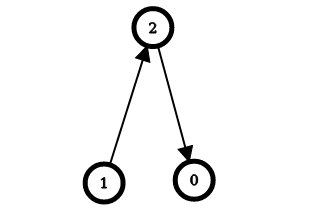
Input: n = 3, edges = [[1,2],[2,0]]

Output: [2,0,1]

Explanation: The image above shows the graph formed by the edges.

For node 0: after reversing the edges [2,0] and [1,2], it is possible to reach any other node starting from node 0.

So, answer[0] = 2.

For node 1: it is already possible to reach any other node starting from node 1.

So, answer[1] = 0.

For node 2: after reversing the edge [1, 2], it is possible to reach any other node starting from node 2.

So, answer[2] = 1.

Constraints:

• 2 <= n <= 105
• edges.length == n - 1
• edges[i].length == 2
• 0 <= ui == edges[i][0] < n
• 0 <= vi == edges[i][1] < n
• ui != vi
• The input is generated such that if the edges were bi-directional, the graph would be a tree.

Solution

import java.util.LinkedList
import java.util.Queue

class Solution {
    fun minEdgeReversals(n: Int, edges: Array<IntArray>): IntArray {
        val nexts: Array<MutableList<IntArray>> = Array(n) { ArrayList() }
        for (edge in edges) {
            val u = edge[0]
            val v = edge[1]
            nexts[u].add(intArrayOf(1, v))
            nexts[v].add(intArrayOf(-1, u))
        }
        val res = IntArray(n)
        for (i in 0 until n) {
            res[i] = -1
        }
        res[0] = dfs(nexts, 0, -1)
        val queue: Queue<Int> = LinkedList()
        queue.add(0)
        while (queue.isNotEmpty()) {
            val index = queue.remove()
            val `val` = res[index]
            val next: List<IntArray> = nexts[index]
            for (node in next) {
                if (res[node[1]] == -1) {
                    if (node[0] == 1) {
                        res[node[1]] = `val` + 1
                    } else {
                        res[node[1]] = `val` - 1
                    }
                    queue.add(node[1])
                }
            }
        }
        return res
    }

    private fun dfs(nexts: Array<MutableList<IntArray>>, index: Int, pre: Int): Int {
        var res = 0
        val next: List<IntArray> = nexts[index]
        for (node in next) {
            if (node[1] != pre) {
                if (node[0] == -1) {
                    res++
                }
                res += dfs(nexts, node[1], index)
            }
        }
        return res
    }
}

This site is open source. Improve this page.