LeetCode in Kotlin

2718. Sum of Matrix After Queries

Medium

You are given an integer n and a 0-indexed 2D array queries where queries[i] = [typei, indexi, vali].

Initially, there is a 0-indexed n x n matrix filled with 0’s. For each query, you must apply one of the following changes:

• if typei == 0, set the values in the row with indexi to vali, overwriting any previous values.
• if typei == 1, set the values in the column with indexi to vali, overwriting any previous values.

Return the sum of integers in the matrix after all queries are applied.

Example 1:

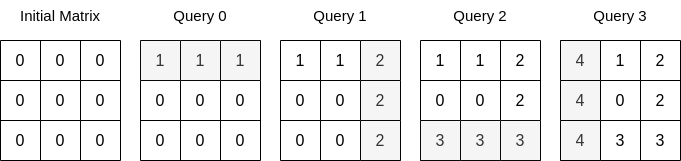
Input: n = 3, queries = [[0,0,1],[1,2,2],[0,2,3],[1,0,4]]

Output: 23

Explanation: The image above describes the matrix after each query. The sum of the matrix after all queries are applied is 23.

Example 2:

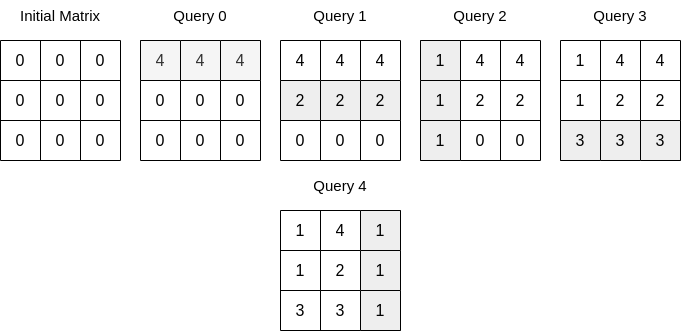
Input: n = 3, queries = [[0,0,4],[0,1,2],[1,0,1],[0,2,3],[1,2,1]]

Output: 17

Explanation: The image above describes the matrix after each query. The sum of the matrix after all queries are applied is 17.

Constraints:

• 1 <= n <= 104
• 1 <= queries.length <= 5 * 104
• queries[i].length == 3
• 0 <= typei <= 1
• 0 <= indexi < n
• 0 <= vali <= 105

Solution

class Solution {
    fun matrixSumQueries(n: Int, queries: Array<IntArray>): Long {
        val queriedRow = BooleanArray(n)
        val queriedCol = BooleanArray(n)
        var sum: Long = 0
        var remainingRows = n
        var remainingCols = n
        for (i in queries.indices.reversed()) {
            val type = queries[i][0]
            val index = queries[i][1]
            val value = queries[i][2]
            if (type == 0) {
                if (queriedRow[index]) {
                    continue
                }
                sum += (value * remainingCols).toLong()
                remainingRows--
                queriedRow[index] = true
            } else {
                if (queriedCol[index]) {
                    continue
                }
                sum += (value * remainingRows).toLong()
                remainingCols--
                queriedCol[index] = true
            }
        }
        return sum
    }
}

This site is open source. Improve this page.