LeetCode in Kotlin

2684. Maximum Number of Moves in a Grid

Medium

You are given a 0-indexed m x n matrix grid consisting of positive integers.

You can start at any cell in the first column of the matrix, and traverse the grid in the following way:

• From a cell (row, col), you can move to any of the cells: (row - 1, col + 1), (row, col + 1) and (row + 1, col + 1) such that the value of the cell you move to, should be strictly bigger than the value of the current cell.

Return the maximum number of moves that you can perform.

Example 1:

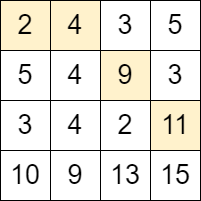
Input: grid = [[2,4,3,5],[5,4,9,3],[3,4,2,11],[10,9,13,15]]

Output: 3

Explanation: We can start at the cell (0, 0) and make the following moves:

• (0, 0) -> (0, 1).
• (0, 1) -> (1, 2).
• (1, 2) -> (2, 3).

It can be shown that it is the maximum number of moves that can be made.

Example 2:

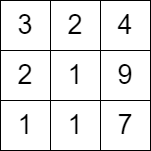Input: grid = [[3,2,4],[2,1,9],[1,1,7]]

Output: 0

Explanation: Starting from any cell in the first column we cannot perform any moves.

Constraints:

• m == grid.length
• n == grid[i].length
• 2 <= m, n <= 1000
• 4 <= m * n <= 105
• 1 <= grid[i][j] <= 106

Solution

class Solution {
    fun maxMoves(grid: Array<IntArray>): Int {
        val h = grid.size
        var dp1 = BooleanArray(h)
        var dp2 = BooleanArray(h)
        var rtn = 0
        dp1.fill(true)
        for (col in 1 until grid[0].size) {
            var f = false
            for (row in 0 until h) {
                val pr = row - 1
                val nr = row + 1
                dp2[row] = false
                if (pr >= 0 && dp1[pr] && grid[pr][col - 1] < grid[row][col]) {
                    dp2[row] = true
                    f = true
                }
                if (nr < h && dp1[nr] && grid[nr][col - 1] < grid[row][col]) {
                    dp2[row] = true
                    f = true
                }
                if (dp1[row] && grid[row][col - 1] < grid[row][col]) {
                    dp2[row] = true
                    f = true
                }
            }
            val t = dp1
            dp1 = dp2
            dp2 = t
            if (!f) break
            rtn++
        }
        return rtn
    }
}

This site is open source. Improve this page.