LeetCode in Kotlin

2658. Maximum Number of Fish in a Grid

Medium

You are given a 0-indexed 2D matrix grid of size m x n, where (r, c) represents:

• A land cell if grid[r][c] = 0, or
• A water cell containing grid[r][c] fish, if grid[r][c] > 0.

A fisher can start at any water cell (r, c) and can do the following operations any number of times:

• Catch all the fish at cell (r, c), or
• Move to any adjacent water cell.

Return the maximum number of fish the fisher can catch if he chooses his starting cell optimally, or 0 if no water cell exists.

An adjacent cell of the cell (r, c), is one of the cells (r, c + 1), (r, c - 1), (r + 1, c) or (r - 1, c) if it exists.

Example 1:

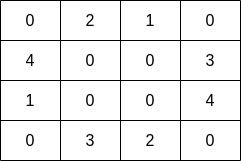
Input: grid = [[0,2,1,0],[4,0,0,3],[1,0,0,4],[0,3,2,0]]

Output: 7

Explanation: The fisher can start at cell (1,3) and collect 3 fish, then move to cell (2,3) and collect 4 fish.

Example 2:

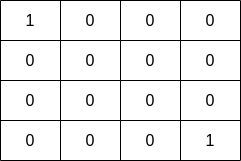
Input: grid = [[1,0,0,0],[0,0,0,0],[0,0,0,0],[0,0,0,1]]

Output: 1

Explanation: The fisher can start at cells (0,0) or (3,3) and collect a single fish.

Constraints:

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 10
• 0 <= grid[i][j] <= 10

Solution

class Solution {
    fun findMaxFish(grid: Array<IntArray>): Int {
        val visited = Array(grid.size) { BooleanArray(grid[0].size) }
        val dir = arrayOf(
            intArrayOf(0, 1),
            intArrayOf(0, -1),
            intArrayOf(1, 0),
            intArrayOf(-1, 0)
        )

        fun isValid(x: Int, y: Int) = x in (0..grid.lastIndex) && y in (0..grid[0].lastIndex) &&
            grid[x][y] != 0 && !visited[x][y]

        fun dfs(x: Int, y: Int): Int {
            if (!isValid(x, y)) {
                return 0
            }
            visited[x][y] = true
            var total = grid[x][y]
            for (d in dir) {
                total += dfs(x + d[0], y + d[1])
            }
            return total
        }

        var res = 0
        for (i in grid.indices) {
            for (j in grid[0].indices) {
                if (grid[i][j] != 0)
                    res = maxOf(res, dfs(i, j))
            }
        }

        return res
    }
}

This site is open source. Improve this page.