LeetCode in Kotlin

2646. Minimize the Total Price of the Trips

Hard

There exists an undirected and unrooted tree with n nodes indexed from 0 to n - 1. You are given the integer n and a 2D integer array edges of length n - 1, where edges[i] = [a_i, b_i] indicates that there is an edge between nodes a_i and b_i in the tree.

Each node has an associated price. You are given an integer array price, where price[i] is the price of the i^th node.

The price sum of a given path is the sum of the prices of all nodes lying on that path.

Additionally, you are given a 2D integer array trips, where trips[i] = [start_i, end_i] indicates that you start the i^th trip from the node start_i and travel to the node end_i by any path you like.

Before performing your first trip, you can choose some non-adjacent nodes and halve the prices.

Return the minimum total price sum to perform all the given trips.

Example 1:

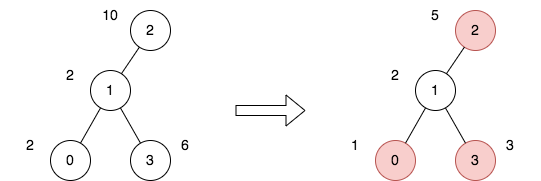
Input: n = 4, edges = [[0,1],[1,2],[1,3]], price = [2,2,10,6], trips = [[0,3],[2,1],[2,3]]

Output: 23

Explanation: The diagram above denotes the tree after rooting it at node 2. The first part shows the initial tree and the second part shows the tree after choosing nodes 0, 2, and 3, and making their price half.

For the 1^st trip, we choose path [0,1,3]. The price sum of that path is 1 + 2 + 3 = 6.

For the 2^nd trip, we choose path [2,1]. The price sum of that path is 2 + 5 = 7.

For the 3^rd trip, we choose path [2,1,3]. The price sum of that path is 5 + 2 + 3 = 10.

The total price sum of all trips is 6 + 7 + 10 = 23.

It can be proven, that 23 is the minimum answer that we can achieve.

Example 2:

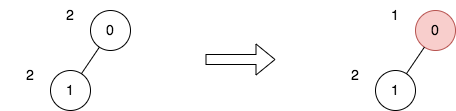
Input: n = 2, edges = [[0,1]], price = [2,2], trips = [[0,0]]

Output: 1

Explanation: The diagram above denotes the tree after rooting it at node 0. The first part shows the initial tree and the second part shows the tree after choosing node 0, and making its price half.

For the 1^st trip, we choose path [0]. The price sum of that path is 1.

The total price sum of all trips is 1. It can be proven, that 1 is the minimum answer that we can achieve.

Constraints:

1 <= n <= 50
edges.length == n - 1
0 <= a_i, b_i <= n - 1
edges represents a valid tree.
price.length == n
price[i] is an even integer.
1 <= price[i] <= 1000
1 <= trips.length <= 100
0 <= start_i, end_i <= n - 1

Solution

class Solution {
    fun minimumTotalPrice(n: Int, edges: Array<IntArray>, price: IntArray, trips: Array<IntArray>): Int {
        val counts = IntArray(n)
        val adj: MutableList<MutableList<Int?>?> = ArrayList()
        for (i in 0 until n) adj.add(ArrayList())
        for (edge in edges) {
            adj[edge[0]]!!.add(edge[1])
            adj[edge[1]]!!.add(edge[0])
        }
        for (trip in trips) {
            val vis = BooleanArray(n)
            dfsTraverse(trip[0], trip[1], counts, adj, vis)
        }
        val dp = IntArray(n)
        for (i in dp.indices) {
            dp[i] = -1
        }
        val paths = BooleanArray(n)
        return dpDFS(n - 1, dp, adj, paths, price, counts)
    }

    private fun dfsTraverse(
        start: Int,
        tgt: Int,
        counts: IntArray,
        adj: MutableList<MutableList<Int?>?>,
        vis: BooleanArray
    ): Boolean {
        if (vis[start]) return false
        vis[start] = true
        if (start == tgt) {
            counts[start]++
            return true
        }
        var ans = false
        for (adjacent in adj[start]!!) {
            ans = ans or dfsTraverse(adjacent!!, tgt, counts, adj, vis)
        }
        if (ans) {
            counts[start]++
        }
        return ans
    }

    private fun dpDFS(
        node: Int,
        dp: IntArray,
        adj: MutableList<MutableList<Int?>?>,
        paths: BooleanArray,
        prices: IntArray,
        counts: IntArray
    ): Int {
        if (paths[node]) return 0
        if (dp[node] != -1) return dp[node]
        var ans1 = 0
        var ans2 = 0
        var childval = 0
        paths[node] = true
        for (child1 in adj[node]!!) {
            if (paths[child1!!]) continue
            paths[child1] = true
            for (child2 in adj[child1]!!) {
                val `val` = dpDFS(child2!!, dp, adj, paths, prices, counts)
                ans2 += `val`
            }
            paths[child1] = false
            childval += counts[child1] * prices[child1]
            ans1 += dpDFS(child1, dp, adj, paths, prices, counts)
        }
        val ans = (ans2 + childval + prices[node] * counts[node] / 2).coerceAtMost(ans1 + prices[node] * counts[node])
        paths[node] = false
        return ans.also { dp[node] = it }
    }
}

This site is open source. Improve this page.