LeetCode in Kotlin

2603. Collect Coins in a Tree

Hard

There exists an undirected and unrooted tree with n nodes indexed from 0 to n - 1. You are given an integer n and a 2D integer array edges of length n - 1, where edges[i] = [a_i, b_i] indicates that there is an edge between nodes a_i and b_i in the tree. You are also given an array coins of size n where coins[i] can be either 0 or 1, where 1 indicates the presence of a coin in the vertex i.

Initially, you choose to start at any vertex in the tree. Then, you can perform the following operations any number of times:

Collect all the coins that are at a distance of at most 2 from the current vertex, or
Move to any adjacent vertex in the tree.

Find the minimum number of edges you need to go through to collect all the coins and go back to the initial vertex.

Note that if you pass an edge several times, you need to count it into the answer several times.

Example 1:

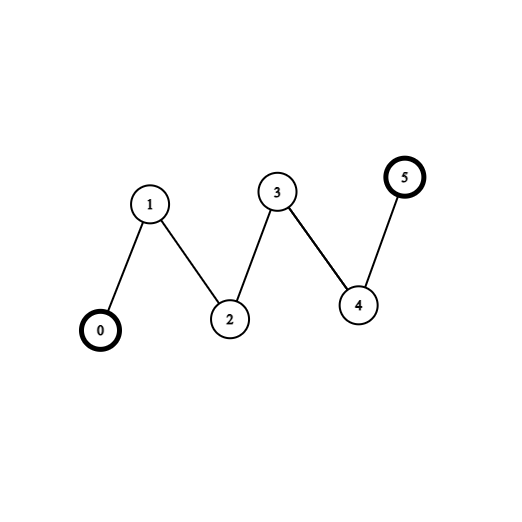
Input: coins = [1,0,0,0,0,1], edges = [[0,1],[1,2],[2,3],[3,4],[4,5]]

Output: 2

Explanation: Start at vertex 2, collect the coin at vertex 0, move to vertex 3, collect the coin at vertex 5 then move back to vertex 2.

Example 2:

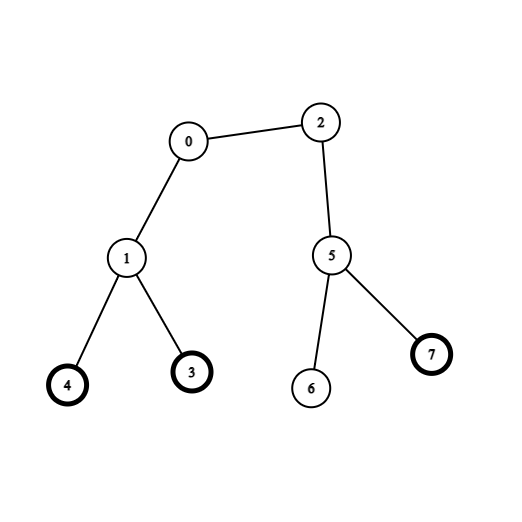
Input: coins = [0,0,0,1,1,0,0,1], edges = [[0,1],[0,2],[1,3],[1,4],[2,5],[5,6],[5,7]]

Output: 2

Explanation: Start at vertex 0, collect the coins at vertices 4 and 3, move to vertex 2, collect the coin at vertex 7, then move back to vertex 0.

Constraints:

n == coins.length
1 <= n <= 3 * 10⁴
0 <= coins[i] <= 1
edges.length == n - 1
edges[i].length == 2
0 <= a_i, b_i < n
a_i != b_i
edges represents a valid tree.

Solution

class Solution {
    private lateinit var coins: IntArray
    private var n = 0
    private lateinit var graph: Array<ArrayList<Int>?>
    private var sum = 0
    private var ret = 0

    fun collectTheCoins(coins: IntArray, edges: Array<IntArray>): Int {
        n = coins.size
        this.coins = coins
        graph = arrayOfNulls(n)
        for (i in 0 until n) {
            graph[i] = ArrayList()
        }
        for (edge in edges) {
            graph[edge[0]]!!.add(edge[1])
            graph[edge[1]]!!.add(edge[0])
        }
        for (coin in coins) {
            sum += coin
        }
        dfs(0, -1)
        return (2 * (ret - 1)).coerceAtLeast(0)
    }

    private fun dfs(node: Int, pre: Int): Int {
        var cnt = 0
        var s = 0
        for (nn in graph[node]!!) {
            if (nn != pre) {
                val r = dfs(nn, node)
                if (r - coins[nn] > 0) cnt++
                s += r
            }
        }
        if (pre != -1 && sum - s - coins[node] - coins[pre] > 0) {
            cnt++
        }
        if (cnt >= 2) {
            ret++
        }
        return s + coins[node]
    }
}

This site is open source. Improve this page.