LeetCode in Kotlin

2596. Check Knight Tour Configuration

Medium

There is a knight on an n x n chessboard. In a valid configuration, the knight starts at the top-left cell of the board and visits every cell on the board exactly once.

You are given an n x n integer matrix grid consisting of distinct integers from the range [0, n * n - 1] where grid[row][col] indicates that the cell (row, col) is the grid[row][col]th cell that the knight visited. The moves are 0-indexed.

Return true if grid represents a valid configuration of the knight’s movements or false otherwise.

Note that a valid knight move consists of moving two squares vertically and one square horizontally, or two squares horizontally and one square vertically. The figure below illustrates all the possible eight moves of a knight from some cell.

Example 1:

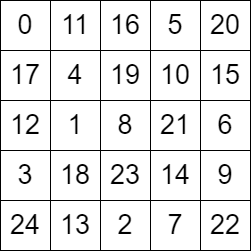
Input: grid = [[0,11,16,5,20],[17,4,19,10,15],[12,1,8,21,6],[3,18,23,14,9],[24,13,2,7,22]]

Output: true

Explanation: The above diagram represents the grid. It can be shown that it is a valid configuration.

Example 2:

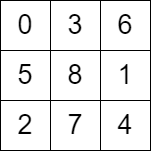
Input: grid = [[0,3,6],[5,8,1],[2,7,4]]

Output: false

Explanation: The above diagram represents the grid. The 8^th move of the knight is not valid considering its position after the 7^th move.

Constraints:

• n == grid.length == grid[i].length
• 3 <= n <= 7
• 0 <= grid[row][col] < n * n
• All integers in grid are unique.

Solution

class Solution {
    fun checkValidGrid(grid: Array<IntArray>): Boolean {
        if (grid[0][0] != 0) {
            return false
        }
        val n = grid.size
        val m = grid[0].size
        val rmove = intArrayOf(2, 2, -2, -2, 1, 1, -1, -1)
        val cmove = intArrayOf(1, -1, 1, -1, 2, -2, 2, -2)
        var cnt = 0
        for (i in 0 until n) {
            for (j in 0 until m) {
                val `val` = grid[i][j]
                var isPoss = false
                for (d in 0..7) {
                    val r = i + rmove[d]
                    val c = j + cmove[d]
                    if (r >= 0 && c >= 0 && r < n && c < m && grid[r][c] == `val` + 1) {
                        isPoss = true
                    }
                }
                if (!isPoss) {
                    cnt++
                }
                if (cnt > 1) return false
            }
        }
        return true
    }
}

This site is open source. Improve this page.