LeetCode in Kotlin

2428. Maximum Sum of an Hourglass

Medium

You are given an m x n integer matrix grid.

We define an hourglass as a part of the matrix with the following form:

Return the maximum sum of the elements of an hourglass.

Note that an hourglass cannot be rotated and must be entirely contained within the matrix.

Example 1:

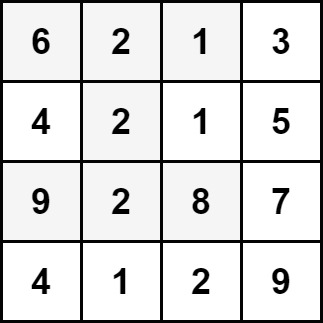
Input: grid = [[6,2,1,3],[4,2,1,5],[9,2,8,7],[4,1,2,9]]

Output: 30

Explanation: The cells shown above represent the hourglass with the maximum sum: 6 + 2 + 1 + 2 + 9 + 2 + 8 = 30.

Example 2:

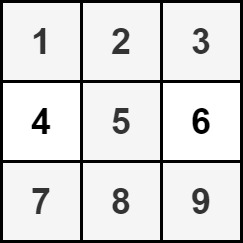
Input: grid = [[1,2,3],[4,5,6],[7,8,9]]

Output: 35

Explanation: There is only one hourglass in the matrix, with the sum: 1 + 2 + 3 + 5 + 7 + 8 + 9 = 35.

Constraints:

• m == grid.length
• n == grid[i].length
• 3 <= m, n <= 150
• 0 <= grid[i][j] <= 106

Solution

class Solution {
    fun maxSum(grid: Array<IntArray>): Int {
        val m = grid.size
        val n = grid[0].size
        var res = 0
        for (i in 0 until m) {
            for (j in 0 until n) {
                res = if (isHourGlass(i, j, m, n)) {
                    res.coerceAtLeast(calculate(i, j, grid))
                } else {
                    // If we cannot form an hour glass from the current row anymore, just move to
                    // the next one
                    break
                }
            }
        }
        return res
    }

    // Check if an hour glass can be formed from the current position
    private fun isHourGlass(r: Int, c: Int, m: Int, n: Int): Boolean {
        return r + 2 < m && c + 2 < n
    }

    // Once we know an hourglass can be formed, just traverse the value
    private fun calculate(r: Int, c: Int, grid: Array<IntArray>): Int {
        var sum = 0
        // Traverse the bottom and the top row of the hour glass at the same time
        for (i in c..c + 2) {
            sum += grid[r][i]
            sum += grid[r + 2][i]
        }
        // Add the middle vlaue
        sum += grid[r + 1][c + 1]
        return sum
    }
}

This site is open source. Improve this page.