LeetCode in Kotlin

2392. Build a Matrix With Conditions

Hard

You are given a positive integer k. You are also given:

• a 2D integer array rowConditions of size n where rowConditions[i] = [abovei, belowi], and
• a 2D integer array colConditions of size m where colConditions[i] = [lefti, righti].

The two arrays contain integers from 1 to k.

You have to build a k x k matrix that contains each of the numbers from 1 to k exactly once. The remaining cells should have the value 0.

The matrix should also satisfy the following conditions:

• The number abovei should appear in a row that is strictly above the row at which the number belowi appears for all i from 0 to n - 1.
• The number lefti should appear in a column that is strictly left of the column at which the number righti appears for all i from 0 to m - 1.

Return any matrix that satisfies the conditions. If no answer exists, return an empty matrix.

Example 1:

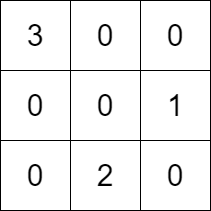
Input: k = 3, rowConditions = [[1,2],[3,2]], colConditions = [[2,1],[3,2]]

Output: [[3,0,0],[0,0,1],[0,2,0]]

Explanation: The diagram above shows a valid example of a matrix that satisfies all the conditions.

The row conditions are the following:

• Number 1 is in row 1, and number 2 is in row 2, so 1 is above 2 in the matrix.

• Number 3 is in row 0, and number 2 is in row 2, so 3 is above 2 in the matrix.

The column conditions are the following:

• Number 2 is in column 1, and number 1 is in column 2, so 2 is left of 1 in the matrix.

• Number 3 is in column 0, and number 2 is in column 1, so 3 is left of 2 in the matrix.

Note that there may be multiple correct answers.

Example 2:

Input: k = 3, rowConditions = [[1,2],[2,3],[3,1],[2,3]], colConditions = [[2,1]]

Output: []

Explanation: From the first two conditions, 3 has to be below 1 but the third conditions needs 3 to be above 1 to be satisfied.

No matrix can satisfy all the conditions, so we return the empty matrix.

Constraints:

• 2 <= k <= 400
• 1 <= rowConditions.length, colConditions.length <= 104
• rowConditions[i].length == colConditions[i].length == 2
• 1 <= abovei, belowi, lefti, righti <= k
• abovei != belowi
• lefti != righti

Solution

import java.util.LinkedList
import java.util.Queue

class Solution {
    // Using topological sort to solve this problem
    fun buildMatrix(k: Int, rowConditions: Array<IntArray>, colConditions: Array<IntArray>): Array<IntArray> {
        // First, get the topo-sorted of row and col
        val row = toposort(k, rowConditions)
        val col = toposort(k, colConditions)
        // base case: when the length of row or col is less than k, return empty.
        // That is: there is a loop in established graph
        if (row.size < k || col.size < k) {
            return Array(0) { IntArray(0) }
        }
        val res = Array(k) { IntArray(k) }
        val map: MutableMap<Int, Int> = HashMap()
        for (i in 0 until k) {
            // we record the number corresbonding to each column:
            // [number, column index]
            map[col[i]] = i
        }
        // col: 3 2 1
        // row: 1 3 2
        for (i in 0 until k) {
            // For each row: we have number row.get(i). And we need to know
            // which column we need to assign, which is from map.get(row.get(i))
            // known by map.get()
            res[i][map[row[i]]!!] = row[i]
        }
        return res
    }

    private fun toposort(k: Int, matrix: Array<IntArray>): List<Int> {
        // need a int[] to record the indegree of each number [1, k]
        val deg = IntArray(k + 1)
        // need a list to record the order of each number, then return this list
        val res: MutableList<Int> = ArrayList()
        // need a 2-D list to be the graph, and fill the graph
        val graph: MutableList<MutableList<Int>> = ArrayList()
        for (i in 0 until k) {
            graph.add(ArrayList())
        }
        // need a queue to do the BFS
        val queue: Queue<Int> = LinkedList()
        // First, we need to establish the graph, following the given matrix
        for (a in matrix) {
            val from = a[0]
            val to = a[1]
            graph[from - 1].add(to)
            deg[to]++
        }
        // Second, after building a graph, we start the bfs,
        // that is, traverse the node with 0 degree
        for (i in 1..k) {
            if (deg[i] == 0) {
                queue.offer(i)
                res.add(i)
            }
        }
        // Third, start the topo sort
        while (queue.isNotEmpty()) {
            val node = queue.poll()
            val list: List<Int> = graph[node - 1]
            for (i in list) {
                if (--deg[i] == 0) {
                    queue.offer(i)
                    res.add(i)
                }
            }
        }
        return res
    }
}

This site is open source. Improve this page.