LeetCode in Kotlin

2368. Reachable Nodes With Restrictions

Medium

There is an undirected tree with n nodes labeled from 0 to n - 1 and n - 1 edges.

You are given a 2D integer array edges of length n - 1 where edges[i] = [ai, bi] indicates that there is an edge between nodes ai and bi in the tree. You are also given an integer array restricted which represents restricted nodes.

Return the maximum number of nodes you can reach from node 0 without visiting a restricted node.

Note that node 0 will not be a restricted node.

Example 1:

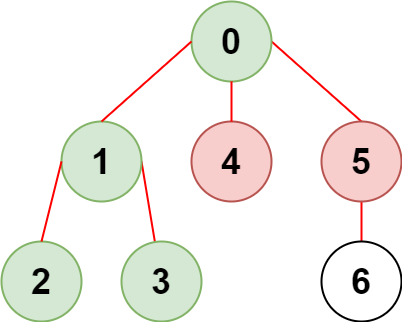
Input: n = 7, edges = [[0,1],[1,2],[3,1],[4,0],[0,5],[5,6]], restricted = [4,5]

Output: 4

Explanation: The diagram above shows the tree. We have that [0,1,2,3] are the only nodes that can be reached from node 0 without visiting a restricted node.

Example 2:

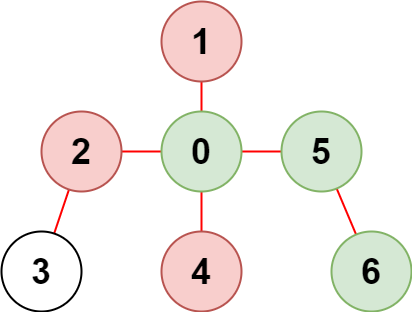
Input: n = 7, edges = [[0,1],[0,2],[0,5],[0,4],[3,2],[6,5]], restricted = [4,2,1]

Output: 3

Explanation: The diagram above shows the tree. We have that [0,5,6] are the only nodes that can be reached from node 0 without visiting a restricted node.

Constraints:

• 2 <= n <= 105
• edges.length == n - 1
• edges[i].length == 2
• 0 <= ai, bi < n
• ai != bi
• edges represents a valid tree.
• 1 <= restricted.length < n
• 1 <= restricted[i] < n
• All the values of restricted are unique.

Solution

import java.util.ArrayDeque
import java.util.Queue

class Solution {
    fun reachableNodes(n: Int, edges: Array<IntArray>, restricted: IntArray): Int {
        val graph: Array<MutableList<Int>?> = arrayOfNulls(n)
        for (i in 0 until n) {
            graph[i] = ArrayList()
        }
        for (edge in edges) {
            val src = edge[0]
            val dest = edge[1]
            graph[src]?.add(dest)
            graph[dest]?.add(src)
        }
        val q: Queue<Int> = ArrayDeque()
        val visited = BooleanArray(n)
        q.offer(0)
        visited[0] = true
        for (node in restricted) {
            visited[node] = true
        }
        var ans = 0
        while (q.isNotEmpty()) {
            val vertex = q.poll()
            ans++
            for (neighbour in graph[vertex]!!) {
                if (!visited[neighbour]) {
                    q.offer(neighbour)
                    visited[neighbour] = true
                }
            }
        }
        return ans
    }
}

This site is open source. Improve this page.