LeetCode in Kotlin

2280. Minimum Lines to Represent a Line Chart

Medium

You are given a 2D integer array stockPrices where stockPrices[i] = [dayi, pricei] indicates the price of the stock on day dayi is pricei. A line chart is created from the array by plotting the points on an XY plane with the X-axis representing the day and the Y-axis representing the price and connecting adjacent points. One such example is shown below:

Return the minimum number of lines needed to represent the line chart.

Example 1:

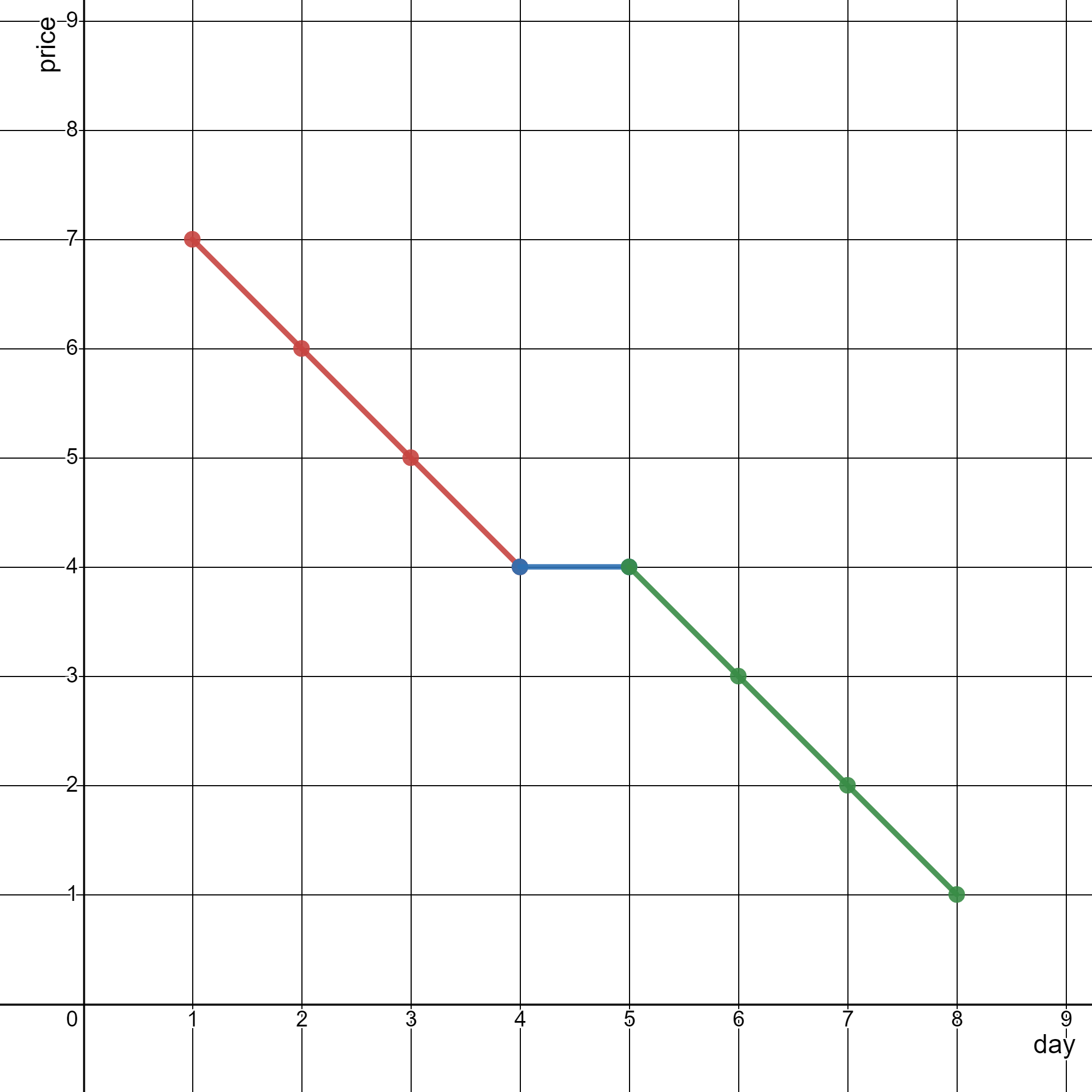
Input: stockPrices = [[1,7],[2,6],[3,5],[4,4],[5,4],[6,3],[7,2],[8,1]]

Output: 3

Explanation:

The diagram above represents the input, with the X-axis representing the day and Y-axis representing the price.

The following 3 lines can be drawn to represent the line chart:

• Line 1 (in red) from (1,7) to (4,4) passing through (1,7), (2,6), (3,5), and (4,4).

• Line 2 (in blue) from (4,4) to (5,4).

• Line 3 (in green) from (5,4) to (8,1) passing through (5,4), (6,3), (7,2), and (8,1).

It can be shown that it is not possible to represent the line chart using less than 3 lines.

Example 2:

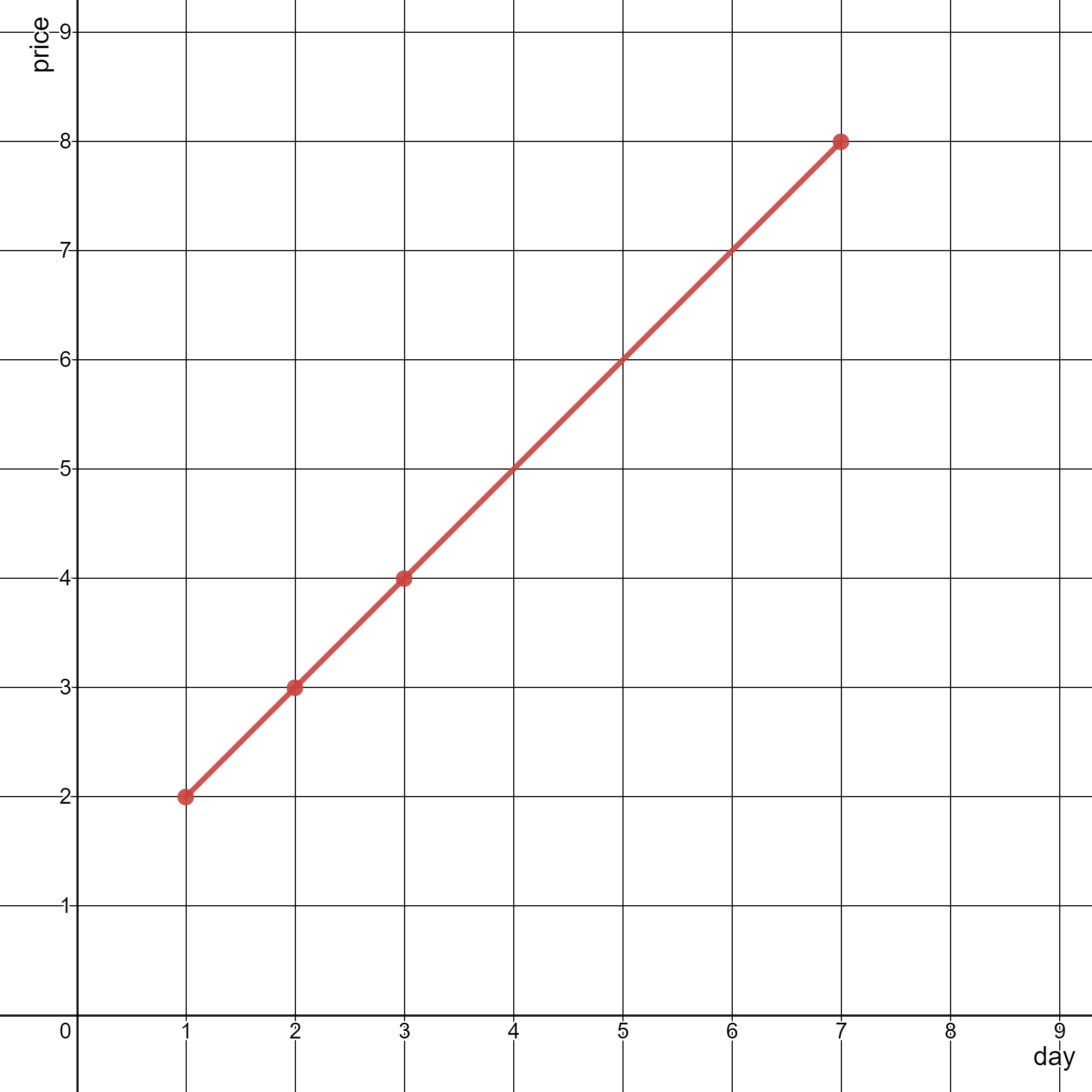
Input: stockPrices = [[3,4],[1,2],[7,8],[2,3]]

Output: 1

Explanation: As shown in the diagram above, the line chart can be represented with a single line.

Constraints:

• 1 <= stockPrices.length <= 105
• stockPrices[i].length == 2
• 1 <= dayi, pricei <= 109
• All dayi are distinct.

Solution

class Solution {
    fun minimumLines(stockPrices: Array<IntArray>): Int {
        if (stockPrices.size == 1) {
            return 0
        }
        stockPrices.sortWith { a: IntArray, b: IntArray -> a[0] - b[0] }
        // multiply with 1.0 to make it double and multiply with 100 for making it big so that
        // difference won't come out to be very less and after division it become 0.
        // failing for one of the case without multiply 100
        var lastSlope = (
            (stockPrices[1][1] - stockPrices[0][1]) *
                100 /
                ((stockPrices[1][0] - stockPrices[0][0]) * 1.0)
            )
        var ans = 1
        for (i in 2 until stockPrices.size) {
            val curSlope = (
                (stockPrices[i][1] - stockPrices[i - 1][1]) *
                    100 /
                    ((stockPrices[i][0] - stockPrices[i - 1][0]) * 1.0)
                )
            if (lastSlope != curSlope) {
                lastSlope = curSlope
                ans++
            }
        }
        return ans
    }
}

This site is open source. Improve this page.