LeetCode in Kotlin

1840. Maximum Building Height

Hard

You want to build n new buildings in a city. The new buildings will be built in a line and are labeled from 1 to n.

However, there are city restrictions on the heights of the new buildings:

• The height of each building must be a non-negative integer.
• The height of the first building must be 0.
• The height difference between any two adjacent buildings cannot exceed 1.

Additionally, there are city restrictions on the maximum height of specific buildings. These restrictions are given as a 2D integer array restrictions where restrictions[i] = [idi, maxHeighti] indicates that building idi must have a height less than or equal to maxHeighti.

It is guaranteed that each building will appear at most once in restrictions, and building 1 will not be in restrictions.

Return the maximum possible height of the tallest building.

Example 1:

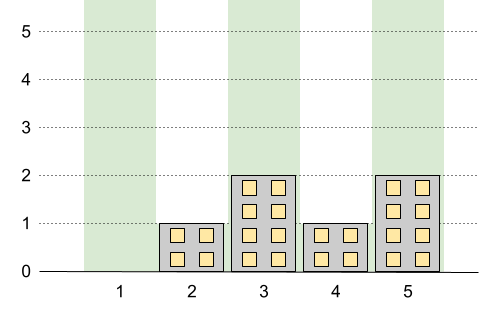
Input: n = 5, restrictions = [[2,1],[4,1]]

Output: 2

Explanation: The green area in the image indicates the maximum allowed height for each building. We can build the buildings with heights [0,1,2,1,2], and the tallest building has a height of 2.

Example 2:

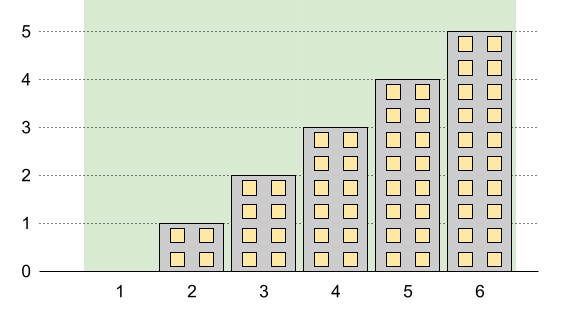
Input: n = 6, restrictions = []

Output: 5

Explanation: The green area in the image indicates the maximum allowed height for each building. We can build the buildings with heights [0,1,2,3,4,5], and the tallest building has a height of 5.

Example 3:

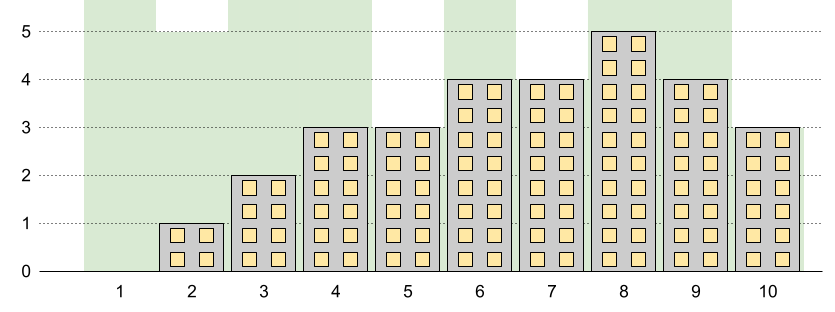
Input: n = 10, restrictions = [[5,3],[2,5],[7,4],[10,3]]

Output: 5

Explanation: The green area in the image indicates the maximum allowed height for each building. We can build the buildings with heights [0,1,2,3,3,4,4,5,4,3], and the tallest building has a height of 5.

Constraints:

• 2 <= n <= 109
• 0 <= restrictions.length <= min(n - 1, 105)
• 2 <= idi <= n
• idi is unique.
• 0 <= maxHeighti <= 109

Solution

class Solution {
    fun maxBuilding(n: Int, restrictions: Array<IntArray>): Int {
        if (restrictions.isEmpty()) {
            return n - 1
        }
        val m = restrictions.size
        restrictions.sortWith(compareBy { a: IntArray -> a[0] })
        for (i in m - 2 downTo 0) {
            restrictions[i][1] =
                restrictions[i][1].coerceAtMost(restrictions[i + 1][1] + restrictions[i + 1][0] - restrictions[i][0])
        }
        var id = 1
        var height = 0
        var res = 0
        for (r in restrictions) {
            var currMax: Int
            if (r[1] >= height + r[0] - id) {
                currMax = height + r[0] - id
                height = currMax
            } else {
                currMax = (height + r[0] - id + r[1]) / 2
                height = r[1]
            }
            id = r[0]
            res = res.coerceAtLeast(currMax)
        }
        if (id != n) {
            res = res.coerceAtLeast(height + n - id)
        }
        return res
    }
}

This site is open source. Improve this page.