LeetCode in Kotlin

1659. Maximize Grid Happiness

Hard

You are given four integers, m, n, introvertsCount, and extrovertsCount. You have an m x n grid, and there are two types of people: introverts and extroverts. There are introvertsCount introverts and extrovertsCount extroverts.

You should decide how many people you want to live in the grid and assign each of them one grid cell. Note that you do not have to have all the people living in the grid.

The happiness of each person is calculated as follows:

• Introverts start with 120 happiness and lose 30 happiness for each neighbor (introvert or extrovert).
• Extroverts start with 40 happiness and gain 20 happiness for each neighbor (introvert or extrovert).

Neighbors live in the directly adjacent cells north, east, south, and west of a person’s cell.

The grid happiness is the sum of each person’s happiness. Return the maximum possible grid happiness.

Example 1:

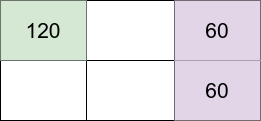
Input: m = 2, n = 3, introvertsCount = 1, extrovertsCount = 2

Output: 240

Explanation: Assume the grid is 1-indexed with coordinates (row, column).

We can put the introvert in cell (1,1) and put the extroverts in cells (1,3) and (2,3).

• Introvert at (1,1) happiness: 120 (starting happiness) - (0 * 30) (0 neighbors) = 120

• Extrovert at (1,3) happiness: 40 (starting happiness) + (1 * 20) (1 neighbor) = 60

• Extrovert at (2,3) happiness: 40 (starting happiness) + (1 * 20) (1 neighbor) = 60

The grid happiness is 120 + 60 + 60 = 240.

The above figure shows the grid in this example with each person’s happiness. The introvert stays in the light green cell while the extroverts live on the light purple cells.

Example 2:

Input: m = 3, n = 1, introvertsCount = 2, extrovertsCount = 1

Output: 260

Explanation: Place the two introverts in (1,1) and (3,1) and the extrovert at (2,1).

• Introvert at (1,1) happiness: 120 (starting happiness) - (1 * 30) (1 neighbor) = 90

• Extrovert at (2,1) happiness: 40 (starting happiness) + (2 * 20) (2 neighbors) = 80

• Introvert at (3,1) happiness: 120 (starting happiness) - (1 * 30) (1 neighbor) = 90

The grid happiness is 90 + 80 + 90 = 260.

Example 3:

Input: m = 2, n = 2, introvertsCount = 4, extrovertsCount = 0

Output: 240

Constraints:

• 1 <= m, n <= 5
• 0 <= introvertsCount, extrovertsCount <= min(m * n, 6)

Solution

import kotlin.math.max

@Suppress("kotlin:S107")
class Solution {
    private fun maxHappiness(
        index: Int,
        m: Int,
        n: Int,
        introverts: Int,
        extroverts: Int,
        board: Int,
        dp: Array<Array<Array<IntArray>>>,
        tmask: Int,
    ): Int {
        if (index >= m * n) {
            return 0
        }
        if (dp[index][introverts][extroverts][board] != 0) {
            return dp[index][introverts][extroverts][board]
        }
        var introScore = -1
        var extroScore = -1
        if (introverts > 0) {
            val newBoard = ((board shl 2) or INTROVERT) and tmask
            introScore =
                (
                    120 +
                        adjust(board, INTROVERT, n, index) +
                        maxHappiness(
                            index + 1,
                            m,
                            n,
                            introverts - 1,
                            extroverts,
                            newBoard,
                            dp,
                            tmask,
                        )
                    )
        }
        if (extroverts > 0) {
            val newBoard = ((board shl 2) or EXTROVERT) and tmask
            extroScore =
                (
                    40 +
                        adjust(board, EXTROVERT, n, index) +
                        maxHappiness(
                            index + 1,
                            m,
                            n,
                            introverts,
                            extroverts - 1,
                            newBoard,
                            dp,
                            tmask,
                        )
                    )
        }
        val newBoard = ((board shl 2) or NONE) and tmask
        val skip = maxHappiness(index + 1, m, n, introverts, extroverts, newBoard, dp, tmask)
        dp[index][introverts][extroverts][board] =
            max(skip, max(introScore, extroScore))
        return dp[index][introverts][extroverts][board]
    }

    private fun adjust(board: Int, thisIs: Int, col: Int, index: Int): Int {
        val shiftBy = 2 * (col - 1)
        var left = board and 0x03
        if (index % col == 0) {
            left = NONE
        }
        val up = (board shr shiftBy) and 0x03
        val combination = intArrayOf(left, up)
        var adjustment = 0
        for (neighbor in combination) {
            if (neighbor == NONE) {
                continue
            }
            if (neighbor == INTROVERT && thisIs == INTROVERT) {
                adjustment -= 60
            } else if (neighbor == INTROVERT && thisIs == EXTROVERT) {
                adjustment -= 10
            } else if (neighbor == EXTROVERT && thisIs == INTROVERT) {
                adjustment -= 10
            } else if (neighbor == EXTROVERT && thisIs == EXTROVERT) {
                adjustment += 40
            }
        }
        return adjustment
    }

    fun getMaxGridHappiness(m: Int, n: Int, introvertsCount: Int, extrovertsCount: Int): Int {
        val dp = Array<Array<Array<IntArray>>>(m * n) {
            Array<Array<IntArray>>(introvertsCount + 1) {
                Array<IntArray>(extrovertsCount + 1) { IntArray((1 shl (2 * n))) }
            }
        }
        val tmask = (1 shl (2 * n)) - 1
        return maxHappiness(0, m, n, introvertsCount, extrovertsCount, 0, dp, tmask)
    }

    companion object {
        private const val NONE = 0
        private const val INTROVERT = 1
        private const val EXTROVERT = 2
    }
}

This site is open source. Improve this page.