LeetCode in Kotlin

1514. Path with Maximum Probability

Medium

You are given an undirected weighted graph of n nodes (0-indexed), represented by an edge list where edges[i] = [a, b] is an undirected edge connecting the nodes a and b with a probability of success of traversing that edge succProb[i].

Given two nodes start and end, find the path with the maximum probability of success to go from start to end and return its success probability.

If there is no path from start to end, return 0. Your answer will be accepted if it differs from the correct answer by at most 1e-5.

Example 1:

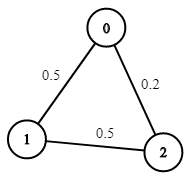
Input: n = 3, edges = [[0,1],[1,2],[0,2]], succProb = [0.5,0.5,0.2], start = 0, end = 2

Output: 0.25000

Explanation: There are two paths from start to end, one having a probability of success = 0.2 and the other has 0.5 * 0.5 = 0.25.

Example 2:

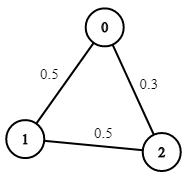
Input: n = 3, edges = [[0,1],[1,2],[0,2]], succProb = [0.5,0.5,0.3], start = 0, end = 2

Output: 0.30000

Example 3:

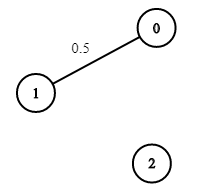
Input: n = 3, edges = [[0,1]], succProb = [0.5], start = 0, end = 2

Output: 0.00000

Explanation: There is no path between 0 and 2.

Constraints:

• 2 <= n <= 10^4
• 0 <= start, end < n
• start != end
• 0 <= a, b < n
• a != b
• 0 <= succProb.length == edges.length <= 2*10^4
• 0 <= succProb[i] <= 1
• There is at most one edge between every two nodes.

Solution

import java.util.ArrayDeque
import java.util.Queue

class Solution {
    fun maxProbability(n: Int, edges: Array<IntArray>, succProb: DoubleArray, start: Int, end: Int): Double {
        val nodeToNodesList: Array<MutableList<Int>?> = arrayOfNulls(n)
        val nodeToProbabilitiesList: Array<MutableList<Double>?> = arrayOfNulls(n)
        for (i in 0 until n) {
            nodeToNodesList[i] = mutableListOf()
            nodeToProbabilitiesList[i] = ArrayList()
        }
        for (i in edges.indices) {
            val u = edges[i][0]
            val v = edges[i][1]
            val w = succProb[i]
            nodeToNodesList[u]?.add(v)
            nodeToProbabilitiesList[u]?.add(w)
            nodeToNodesList[v]?.add(u)
            nodeToProbabilitiesList[v]?.add(w)
        }
        val probabilities = DoubleArray(n)
        probabilities[start] = 1.0
        val visited = BooleanArray(n)
        val queue: Queue<Int> = ArrayDeque()
        queue.add(start)
        visited[start] = true
        while (queue.isNotEmpty()) {
            val u = queue.poll()
            visited[u] = false
            for (i in nodeToNodesList[u]?.indices!!) {
                val v = nodeToNodesList[u]?.get(i)
                val w = nodeToProbabilitiesList[u]?.get(i)
                if (probabilities[u] * w!! > probabilities[v!!]) {
                    probabilities[v] = probabilities[u] * w
                    if (!visited[v]) {
                        visited[v] = true
                        queue.add(v)
                    }
                }
            }
        }
        return probabilities[end]
    }
}

This site is open source. Improve this page.