LeetCode in Kotlin

1504. Count Submatrices With All Ones

Medium

Given an m x n binary matrix mat, return the number of submatrices that have all ones.

Example 1:

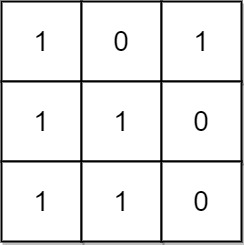
Input: mat = [[1,0,1],[1,1,0],[1,1,0]]

Output: 13

Explanation:

There are 6 rectangles of side 1x1.

There are 2 rectangles of side 1x2.

There are 3 rectangles of side 2x1.

There is 1 rectangle of side 2x2.

There is 1 rectangle of side 3x1.

Total number of rectangles = 6 + 2 + 3 + 1 + 1 = 13.

Example 2:

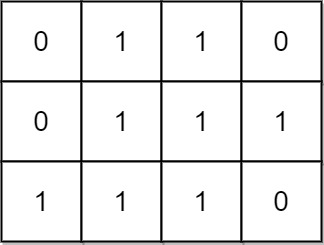
Input: mat = [[0,1,1,0],[0,1,1,1],[1,1,1,0]]

Output: 24

Explanation:

There are 8 rectangles of side 1x1.

There are 5 rectangles of side 1x2.

There are 2 rectangles of side 1x3.

There are 4 rectangles of side 2x1.

There are 2 rectangles of side 2x2.

There are 2 rectangles of side 3x1.

There is 1 rectangle of side 3x2.

Total number of rectangles = 8 + 5 + 2 + 4 + 2 + 2 + 1 = 24.

Constraints:

• 1 <= m, n <= 150
• mat[i][j] is either 0 or 1.

Solution

class Solution {
    fun numSubmat(mat: Array<IntArray>): Int {
        val dp = Array(mat.size) { IntArray(mat[0].size) }
        for (i in mat.indices) {
            var c = 0
            for (j in mat[0].indices.reversed()) {
                if (mat[i][j] == 1) {
                    c++
                } else {
                    c = 0
                }
                dp[i][j] = c
            }
        }
        var ans = 0
        for (i in mat.indices) {
            for (j in mat[0].indices) {
                var x = Int.MAX_VALUE
                for (k in i until mat.size) {
                    x = Math.min(x, dp[k][j])
                    ans += x
                }
            }
        }
        return ans
    }
}

This site is open source. Improve this page.