LeetCode in Kotlin
1373. Maximum Sum BST in Binary Tree
Hard
Given a binary tree root, return the maximum sum of all keys of any sub-tree which is also a Binary Search Tree (BST).
Assume a BST is defined as follows:
- The left subtree of a node contains only nodes with keys less than the node’s key.
- The right subtree of a node contains only nodes with keys greater than the node’s key.
- Both the left and right subtrees must also be binary search trees.
Example 1:
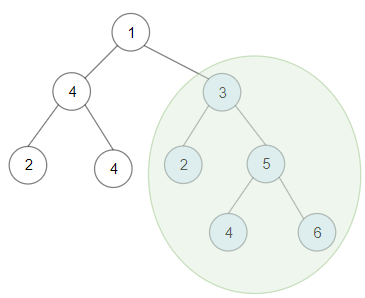
Input: root = [1,4,3,2,4,2,5,null,null,null,null,null,null,4,6]
Output: 20
Explanation: Maximum sum in a valid Binary search tree is obtained in root node with key equal to 3.
Example 2:
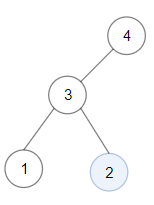
Input: root = [4,3,null,1,2]
Output: 2
Explanation: Maximum sum in a valid Binary search tree is obtained in a single root node with key equal to 2.
Example 3:
Input: root = [-4,-2,-5]
Output: 0
Explanation: All values are negatives. Return an empty BST.
Constraints:
- The number of nodes in the tree is in the range
[1, 4 * 104]. -4 * 104 <= Node.val <= 4 * 104
Solution
import com_github_leetcode.TreeNode
/*
* Example:
* var ti = TreeNode(5)
* var v = ti.`val`
* Definition for a binary tree node.
* class TreeNode(var `val`: Int) {
* var left: TreeNode? = null
* var right: TreeNode? = null
* }
*/
class Solution {
fun maxSumBST(root: TreeNode?): Int {
val temp = checkBST(root)
return Math.max(temp.maxSum, 0)
}
private class IsBST {
var max = Int.MIN_VALUE
var min = Int.MAX_VALUE
var isBst = true
var sum = 0
var maxSum = Int.MIN_VALUE
}
private fun checkBST(root: TreeNode?): IsBST {
if (root == null) {
return IsBST()
}
val lp = checkBST(root.left)
val rp = checkBST(root.right)
val mp = IsBST()
mp.max = Math.max(root.`val`, Math.max(lp.max, rp.max))
mp.min = Math.min(root.`val`, Math.min(lp.min, rp.min))
mp.sum = lp.sum + rp.sum + root.`val`
val check = root.`val` > lp.max && root.`val` < rp.min
if (lp.isBst && rp.isBst && check) {
mp.isBst = true
val tempMax = Math.max(mp.sum, Math.max(lp.sum, rp.sum))
mp.maxSum = Math.max(tempMax, Math.max(lp.maxSum, rp.maxSum))
} else {
mp.isBst = false
mp.maxSum = Math.max(lp.maxSum, rp.maxSum)
}
return mp
}
}

