LeetCode in Kotlin

1252. Cells with Odd Values in a Matrix

Easy

There is an m x n matrix that is initialized to all 0’s. There is also a 2D array indices where each indices[i] = [ri, ci] represents a 0-indexed location to perform some increment operations on the matrix.

For each location indices[i], do both of the following:

1. Increment all the cells on row ri.
2. Increment all the cells on column ci.

Given m, n, and indices, return the number of odd-valued cells in the matrix after applying the increment to all locations in indices.

Example 1:

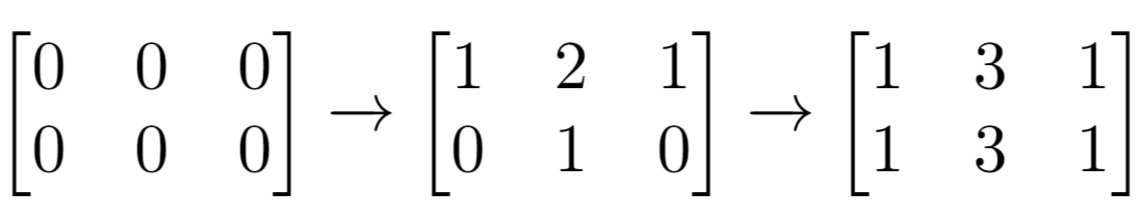
Input: m = 2, n = 3, indices = [[0,1],[1,1]]

Output: 6

Explanation: Initial matrix = [[0,0,0],[0,0,0]].

After applying first increment it becomes [[1,2,1],[0,1,0]].

The final matrix is [[1,3,1],[1,3,1]], which contains 6 odd numbers.

Example 2:

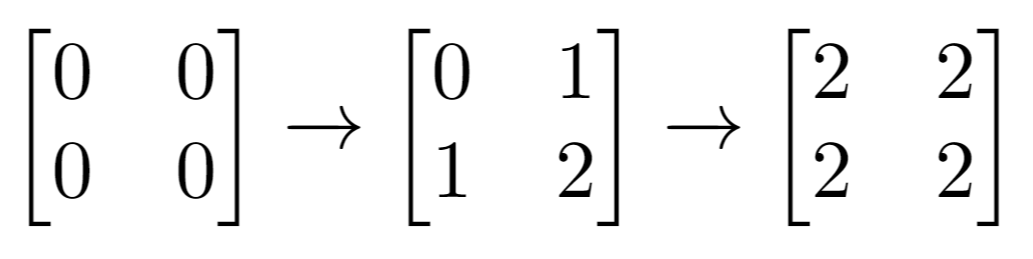
Input: m = 2, n = 2, indices = [[1,1],[0,0]]

Output: 0

Explanation: Final matrix = [[2,2],[2,2]]. There are no odd numbers in the final matrix.

Constraints:

• 1 <= m, n <= 50
• 1 <= indices.length <= 100
• 0 <= ri < m
• 0 <= ci < n

Follow up: Could you solve this in O(n + m + indices.length) time with only O(n + m) extra space?

Solution

class Solution {
    fun oddCells(n: Int, m: Int, indices: Array<IntArray>): Int {
        val matrix = Array(n) { IntArray(m) }
        for (index in indices) {
            addOneToRow(matrix, index[0])
            addOneToColumn(matrix, index[1])
        }
        var oddNumberCount = 0
        for (ints in matrix) {
            for (j in matrix[0].indices) {
                if (ints[j] % 2 != 0) {
                    oddNumberCount++
                }
            }
        }
        return oddNumberCount
    }

    private fun addOneToColumn(matrix: Array<IntArray>, columnIndex: Int) {
        for (i in matrix.indices) {
            matrix[i][columnIndex] += 1
        }
    }

    private fun addOneToRow(matrix: Array<IntArray>, rowIndex: Int) {
        for (j in matrix[0].indices) {
            matrix[rowIndex][j] += 1
        }
    }
}

This site is open source. Improve this page.