LeetCode in Kotlin

1192. Critical Connections in a Network

Hard

There are n servers numbered from 0 to n - 1 connected by undirected server-to-server connections forming a network where connections[i] = [a_i, b_i] represents a connection between servers a_i and b_i. Any server can reach other servers directly or indirectly through the network.

A critical connection is a connection that, if removed, will make some servers unable to reach some other server.

Return all critical connections in the network in any order.

Example 1:

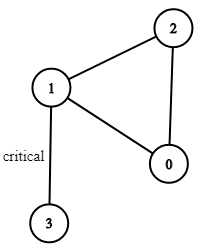
Input: n = 4, connections = [[0,1],[1,2],[2,0],[1,3]]

Output: [[1,3]]

Explanation: [[3,1]] is also accepted.

Example 2:

Input: n = 2, connections = [[0,1]]

Output: [[0,1]]

Constraints:

2 <= n <= 10⁵
n - 1 <= connections.length <= 10⁵
0 <= a_i, b_i <= n - 1
a_i != b_i
There are no repeated connections.

Solution

class Solution {
    fun criticalConnections(n: Int, connections: List<List<Int>>): List<List<Int>> {
        val graph: MutableList<MutableList<Int>> = ArrayList()
        for (i in 0 until n) {
            graph.add(ArrayList())
        }
        // build graph
        for (conn in connections) {
            val x = conn[0]
            val y = conn[1]
            graph[x].add(y)
            graph[y].add(x)
        }
        // record rank
        val rank = IntArray(n)
        // store result
        val res: MutableList<List<Int>> = ArrayList()
        dfs(graph, 0, 1, -1, rank, res)
        return res
    }

    // rank[] records the each node's smallest rank(min (it's natural rank, neighbors's smallest
    // rank))
    private fun dfs(
        graph: List<MutableList<Int>>,
        node: Int,
        time: Int,
        parent: Int,
        rank: IntArray,
        res: MutableList<List<Int>>
    ): Int {
        if (rank[node] > 0) {
            return rank[node]
        }
        // record the current natural rank for current node
        rank[node] = time
        for (nei in graph[node]) {
            // skip the parent, since this is undirected graph
            if (nei == parent) {
                continue
            }
            // step1 : run dfs to get the rank of this nei, if it is visited before, it will reach
            // base case immediately
            val neiTime = dfs(graph, nei, time + 1, node, rank, res)
            // if neiTime is strictly larger than current node's rank, there is no cycle,
            // connections between node and nei is a critically connection.
            if (neiTime > time) {
                res.add(listOf(nei, node))
            }
            // keep updating current node's rank with nei's smaller ranks
            rank[node] = Math.min(rank[node], neiTime)
        }
        // return current node's rank to caller
        return rank[node]
    }
}

This site is open source. Improve this page.