LeetCode in Kotlin

1091. Shortest Path in Binary Matrix

Medium

Given an n x n binary matrix grid, return the length of the shortest clear path in the matrix. If there is no clear path, return -1.

A clear path in a binary matrix is a path from the top-left cell (i.e., (0, 0)) to the bottom-right cell (i.e., (n - 1, n - 1)) such that:

• All the visited cells of the path are 0.
• All the adjacent cells of the path are 8-directionally connected (i.e., they are different and they share an edge or a corner).

The length of a clear path is the number of visited cells of this path.

Example 1:

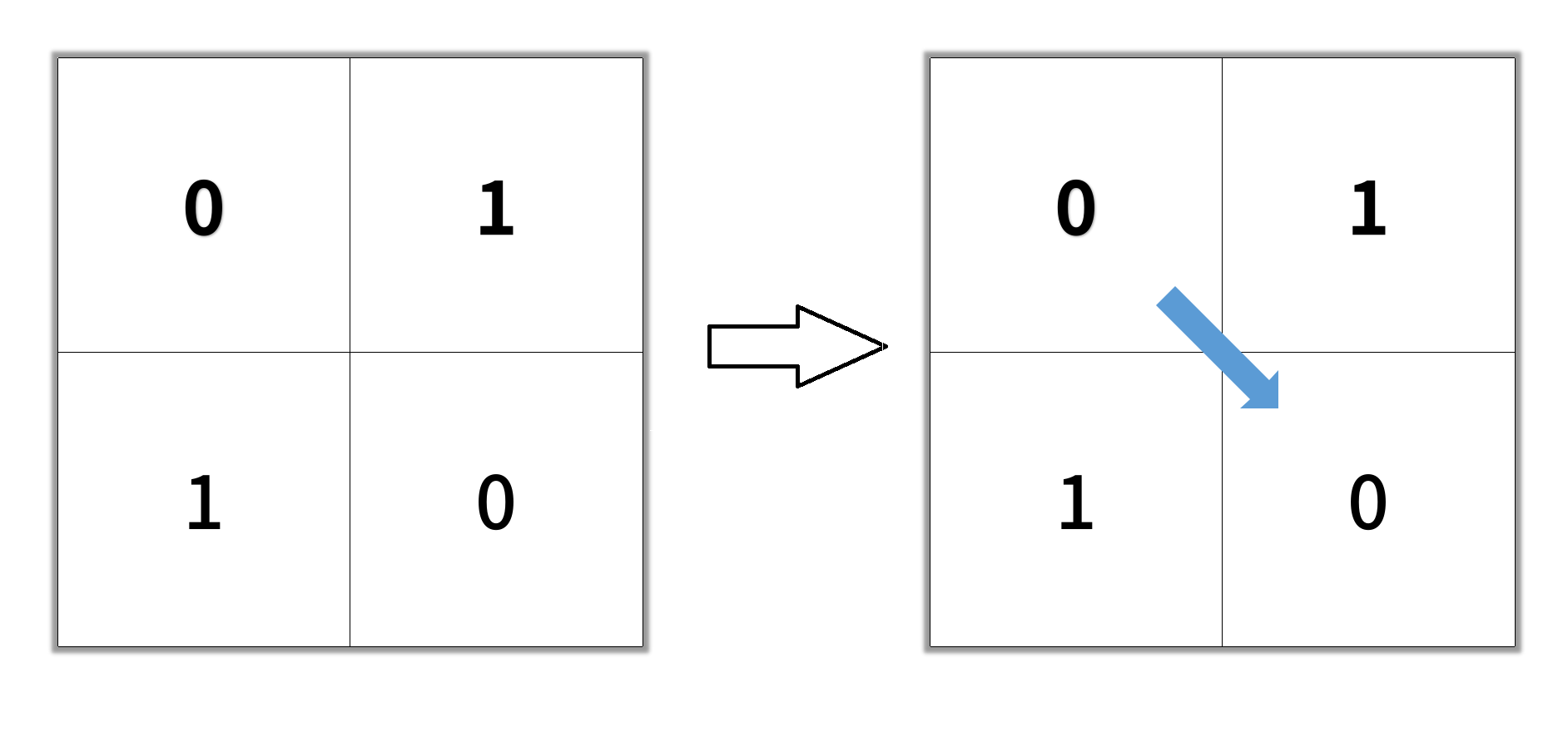
Input: grid = [[0,1],[1,0]]

Output: 2

Example 2:

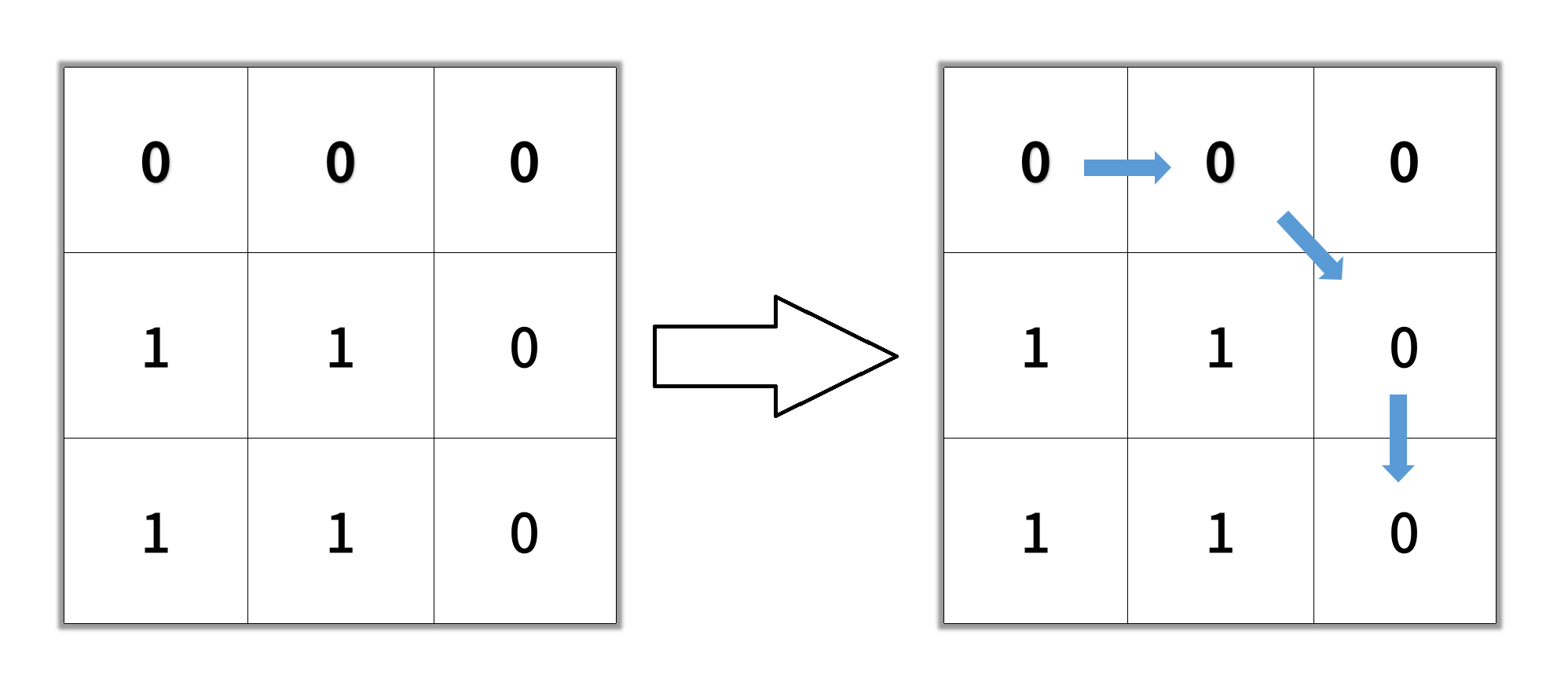
Input: grid = [[0,0,0],[1,1,0],[1,1,0]]

Output: 4

Example 3:

Input: grid = [[1,0,0],[1,1,0],[1,1,0]]

Output: -1

Constraints:

• n == grid.length
• n == grid[i].length
• 1 <= n <= 100
• grid[i][j] is 0 or 1

Solution

import java.util.LinkedList
import java.util.Queue

class Solution {
    private val directions = intArrayOf(0, 1, 1, 0, -1, 1, -1, -1, 0)
    fun shortestPathBinaryMatrix(grid: Array<IntArray>): Int {
        val m = grid.size
        val n = grid[0].size
        if (grid[0][0] == 1 || grid[m - 1][n - 1] == 1) {
            return -1
        }
        var minPath = 0
        val queue: Queue<IntArray> = LinkedList()
        queue.offer(intArrayOf(0, 0))
        val visited = Array(m) { BooleanArray(n) }
        visited[0][0] = true
        while (queue.isNotEmpty()) {
            val size = queue.size
            for (i in 0 until size) {
                val curr = queue.poll()
                if (curr[0] == m - 1 && curr[1] == n - 1) {
                    return minPath + 1
                }
                for (j in 0 until directions.size - 1) {
                    val newx = directions[j] + curr[0]
                    val newy = directions[j + 1] + curr[1]
                    if (newx in 0 until n && newy >= 0 && newy < n && !visited[newx][newy] && grid[newx][newy] == 0) {
                        queue.offer(intArrayOf(newx, newy))
                        visited[newx][newy] = true
                    }
                }
            }
            minPath++
        }
        return -1
    }
}

This site is open source. Improve this page.