LeetCode in Kotlin

1020. Number of Enclaves

Medium

You are given an m x n binary matrix grid, where 0 represents a sea cell and 1 represents a land cell.

A move consists of walking from one land cell to another adjacent (4-directionally) land cell or walking off the boundary of the grid.

Return the number of land cells in grid for which we cannot walk off the boundary of the grid in any number of moves.

Example 1:

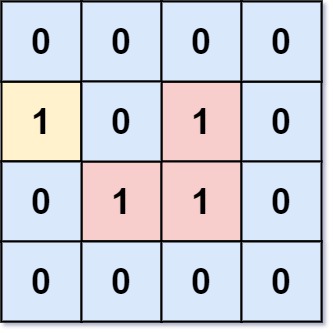
Input: grid = [[0,0,0,0],[1,0,1,0],[0,1,1,0],[0,0,0,0]]

Output: 3

Explanation: There are three 1s that are enclosed by 0s, and one 1 that is not enclosed because its on the boundary.

Example 2:

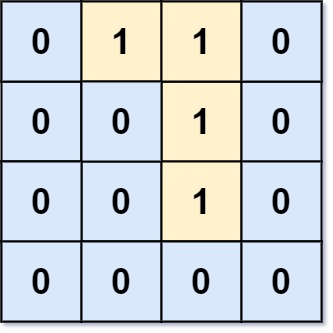
Input: grid = [[0,1,1,0],[0,0,1,0],[0,0,1,0],[0,0,0,0]]

Output: 0

Explanation: All 1s are either on the boundary or can reach the boundary.

Constraints:

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 500
• grid[i][j] is either 0 or 1.

Solution

class Solution {
    private fun walk(a: Array<IntArray>, visited: Array<BooleanArray>, x: Int, y: Int) {
        if (x >= a.size || x < 0 || y >= a[0].size || y < 0) {
            return
        }
        if (visited[x][y]) {
            return
        }
        if (a[x][y] == 0) {
            return
        }
        visited[x][y] = true
        walk(a, visited, x - 1, y)
        walk(a, visited, x, y - 1)
        walk(a, visited, x, y + 1)
        walk(a, visited, x + 1, y)
    }

    fun numEnclaves(a: Array<IntArray>): Int {
        val n = a.size
        val m = a[0].size
        val visited = Array(n) { BooleanArray(m) }
        for (i in 0 until n) {
            walk(a, visited, i, 0)
            walk(a, visited, i, m - 1)
        }
        for (j in 0 until m) {
            walk(a, visited, 0, j)
            walk(a, visited, n - 1, j)
        }
        var unreachables = 0
        for (i in 0 until n) {
            for (j in 0 until m) {
                if (a[i][j] == 1 && !visited[i][j]) {
                    ++unreachables
                }
            }
        }
        return unreachables
    }
}

This site is open source. Improve this page.