LeetCode in Kotlin

913. Cat and Mouse

Hard

A game on an undirected graph is played by two players, Mouse and Cat, who alternate turns.

The graph is given as follows: graph[a] is a list of all nodes b such that ab is an edge of the graph.

The mouse starts at node 1 and goes first, the cat starts at node 2 and goes second, and there is a hole at node 0.

During each player’s turn, they must travel along one edge of the graph that meets where they are. For example, if the Mouse is at node 1, it must travel to any node in graph[1].

Additionally, it is not allowed for the Cat to travel to the Hole (node 0.)

Then, the game can end in three ways:

• If ever the Cat occupies the same node as the Mouse, the Cat wins.
• If ever the Mouse reaches the Hole, the Mouse wins.
• If ever a position is repeated (i.e., the players are in the same position as a previous turn, and it is the same player’s turn to move), the game is a draw.

Given a graph, and assuming both players play optimally, return

• 1 if the mouse wins the game,
• 2 if the cat wins the game, or
• 0 if the game is a draw.

Example 1:

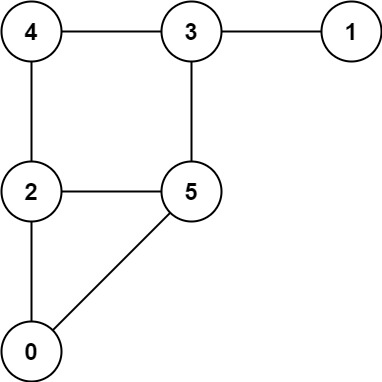
Input: graph = [[2,5],[3],[0,4,5],[1,4,5],[2,3],[0,2,3]]

Output: 0

Example 2:

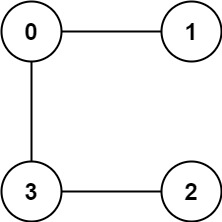
Input: graph = [[1,3],[0],[3],[0,2]]

Output: 1

Constraints:

• 3 <= graph.length <= 50
• 1 <= graph[i].length < graph.length
• 0 <= graph[i][j] < graph.length
• graph[i][j] != i
• graph[i] is unique.
• The mouse and the cat can always move.

Solution

import java.util.LinkedList
import java.util.Queue

class Solution {
    fun catMouseGame(graph: Array<IntArray>): Int {
        val n = graph.size
        val states = Array(n) {
            Array(n) {
                IntArray(
                    2
                )
            }
        }
        val degree = Array(n) {
            Array(n) {
                IntArray(
                    2
                )
            }
        }
        for (m in 0 until n) {
            for (c in 0 until n) {
                degree[m][c][MOUSE] = graph[m].size
                degree[m][c][CAT] = graph[c].size
                for (node in graph[c]) {
                    if (node == 0) {
                        --degree[m][c][CAT]
                        break
                    }
                }
            }
        }
        val q: Queue<IntArray> = LinkedList()
        for (i in 1 until n) {
            states[0][i][MOUSE] = MOUSE_WIN
            states[0][i][CAT] = MOUSE_WIN
            states[i][i][MOUSE] = CAT_WIN
            states[i][i][CAT] = CAT_WIN
            q.offer(intArrayOf(0, i, MOUSE, MOUSE_WIN))
            q.offer(intArrayOf(i, i, MOUSE, CAT_WIN))
            q.offer(intArrayOf(0, i, CAT, MOUSE_WIN))
            q.offer(intArrayOf(i, i, CAT, CAT_WIN))
        }
        while (q.isNotEmpty()) {
            val state = q.poll()
            val mouse = state[0]
            val cat = state[1]
            val turn = state[2]
            val result = state[3]
            if (mouse == 1 && cat == 2 && turn == MOUSE) {
                return result
            }
            val prevTurn = 1 - turn
            for (prev in graph[if (prevTurn == MOUSE) mouse else cat]) {
                val prevMouse = if (prevTurn == MOUSE) prev else mouse
                val prevCat = if (prevTurn == CAT) prev else cat
                if (prevCat != 0 && states[prevMouse][prevCat][prevTurn] == DRAW &&
                    (
                        prevTurn == MOUSE && result == MOUSE_WIN || prevTurn == CAT && result == CAT_WIN ||
                            --degree[prevMouse][prevCat][prevTurn] == 0
                        )
                ) {
                    states[prevMouse][prevCat][prevTurn] = result
                    q.offer(intArrayOf(prevMouse, prevCat, prevTurn, result))
                }
            }
        }
        return DRAW
    }

    companion object {
        private const val DRAW = 0
        private const val MOUSE_WIN = 1
        private const val CAT_WIN = 2
        private const val MOUSE = 0
        private const val CAT = 1
    }
}

This site is open source. Improve this page.