LeetCode in Kotlin

883. Projection Area of 3D Shapes

Easy

You are given an n x n grid where we place some 1 x 1 x 1 cubes that are axis-aligned with the x, y, and z axes.

Each value v = grid[i][j] represents a tower of v cubes placed on top of the cell (i, j).

We view the projection of these cubes onto the xy, yz, and zx planes.

A projection is like a shadow, that maps our 3-dimensional figure to a 2-dimensional plane. We are viewing the “shadow” when looking at the cubes from the top, the front, and the side.

Return the total area of all three projections.

Example 1:

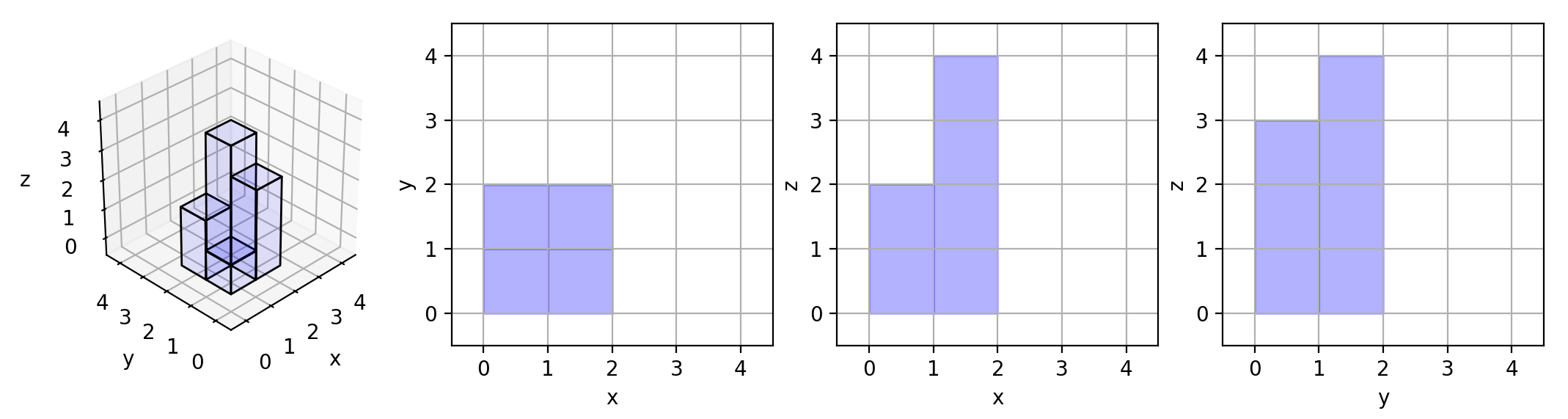
Input: grid = [[1,2],[3,4]]

Output: 17

Explanation: Here are the three projections (“shadows”) of the shape made with each axis-aligned plane.

Example 2:

Input: grid = [[2]]

Output: 5

Example 3:

Input: grid = [[1,0],[0,2]]

Output: 8

Constraints:

• n == grid.length == grid[i].length
• 1 <= n <= 50
• 0 <= grid[i][j] <= 50

Solution

class Solution {
    fun projectionArea(grid: Array<IntArray>): Int {
        val n = grid.size
        val m = grid[0].size
        var sum = n * m
        var count = 0
        for (ints in grid) {
            var max = Int.MIN_VALUE
            for (j in 0 until m) {
                if (ints[j] == 0) {
                    count++
                }
                if (max < ints[j]) {
                    max = ints[j]
                }
            }
            sum += max
        }
        for (i in 0 until n) {
            var max = Int.MIN_VALUE
            for (j in 0 until m) {
                if (max < grid[j][i]) {
                    max = grid[j][i]
                }
            }
            sum += max
        }
        return sum - count
    }
}

This site is open source. Improve this page.