LeetCode in Kotlin
864. Shortest Path to Get All Keys
Hard
You are given an m x n grid grid where:
'.'is an empty cell.'#'is a wall.'@'is the starting point.- Lowercase letters represent keys.
- Uppercase letters represent locks.
You start at the starting point and one move consists of walking one space in one of the four cardinal directions. You cannot walk outside the grid, or walk into a wall.
If you walk over a key, you can pick it up and you cannot walk over a lock unless you have its corresponding key.
For some 1 <= k <= 6, there is exactly one lowercase and one uppercase letter of the first k letters of the English alphabet in the grid. This means that there is exactly one key for each lock, and one lock for each key; and also that the letters used to represent the keys and locks were chosen in the same order as the English alphabet.
Return the lowest number of moves to acquire all keys. If it is impossible, return -1.
Example 1:
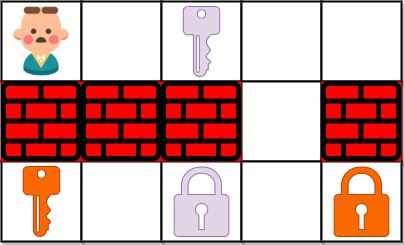
Input: grid = [”@.a.#”,”###.#”,”b.A.B”]
Output: 8
Explanation: Note that the goal is to obtain all the keys not to open all the locks.
Example 2:
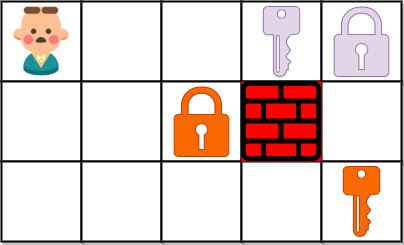
Input: grid = [“@..aA”,”..B#.”,”….b”]
Output: 6
Example 3:

Input: grid = [“@Aa”]
Output: -1
Constraints:
m == grid.lengthn == grid[i].length1 <= m, n <= 30grid[i][j]is either an English letter,'.','#', or'@'.- The number of keys in the grid is in the range
[1, 6]. - Each key in the grid is unique.
- Each key in the grid has a matching lock.
Solution
import java.util.LinkedList
import java.util.Queue
class Solution {
private var m = 0
private var n = 0
fun shortestPathAllKeys(stringGrid: Array<String>): Int {
// strategy: BFS + masking
m = stringGrid.size
n = stringGrid[0].length
val grid = Array(m) { CharArray(n) }
var index = 0
// convert to char Array
for (s in stringGrid) {
grid[index++] = s.toCharArray()
}
// number of keys
var count = 0
val q: Queue<IntArray> = LinkedList()
for (i in 0 until m) {
for (j in 0 until n) {
// find starting position
if (grid[i][j] == '@') {
q.add(intArrayOf(i, j, 0))
}
// count number of keys
if (grid[i][j] in 'a'..'f') {
count++
}
}
}
val dx = intArrayOf(-1, 0, 1, 0)
val dy = intArrayOf(0, -1, 0, 1)
// this is the amt of keys we need
val target = (1 shl count) - 1
// keep track of position and current state
val visited = Array(m) {
Array(n) {
BooleanArray(target + 1)
}
}
// set initial position and state to true
visited[q.peek()[0]][q.peek()[1]][0] = true
var steps = 0
while (q.isNotEmpty()) {
// use size to make sure everything is on one level
var size = q.size
while (--size >= 0) {
val curr = q.poll()
val x = curr[0]
val y = curr[1]
val state = curr[2]
// found all keys
if (state == target) {
return steps
}
for (i in 0..3) {
val nx = x + dx[i]
val ny = y + dy[i]
// use new state so we don't mess up current state
var nState = state
// out of bounds or reached wall
if (!inBounds(nx, ny) || grid[nx][ny] == '#') {
continue
}
// found key
// use OR to add key to our current state because if we already had the key the
// digit would still be 1/true
if (grid[nx][ny] in 'a'..'f') {
// bit mask our found key
nState = state or (1 shl grid[nx][ny] - 'a')
}
// found lock
// use & to see if we have the key
// 0 means that the digit we are looking at is 0
// need a 1 at the digit spot which means there is a key there
if (('A' > grid[nx][ny] || grid[nx][ny] > 'F' || nState and (1 shl grid[nx][ny] - 'A') != 0) &&
!visited[nx][ny][nState]
) {
q.add(intArrayOf(nx, ny, nState))
visited[nx][ny][nState] = true
}
}
}
steps++
}
return -1
}
private fun inBounds(x: Int, y: Int): Boolean {
return x in 0 until m && y >= 0 && y < n
}
}

