LeetCode in Kotlin
662. Maximum Width of Binary Tree
Medium
Given the root of a binary tree, return the maximum width of the given tree.
The maximum width of a tree is the maximum width among all levels.
The width of one level is defined as the length between the end-nodes (the leftmost and rightmost non-null nodes), where the null nodes between the end-nodes that would be present in a complete binary tree extending down to that level are also counted into the length calculation.
It is guaranteed that the answer will in the range of a 32-bit signed integer.
Example 1:
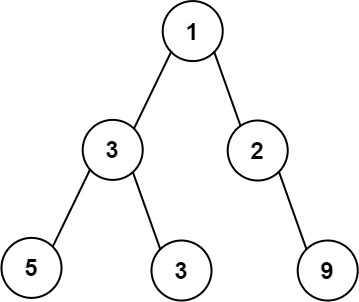
Input: root = [1,3,2,5,3,null,9]
Output: 4
Explanation: The maximum width exists in the third level with length 4 (5,3,null,9).
Example 2:
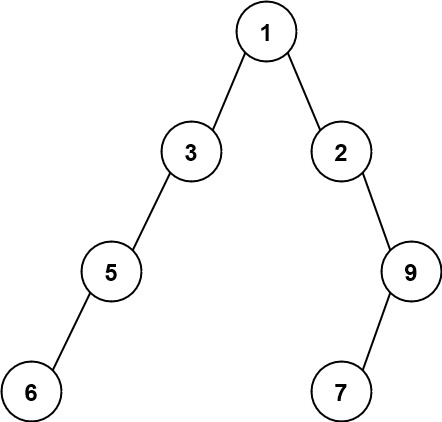
Input: root = [1,3,2,5,null,null,9,6,null,7]
Output: 7
Explanation: The maximum width exists in the fourth level with length 7 (6,null,null,null,null,null,7).
Example 3:
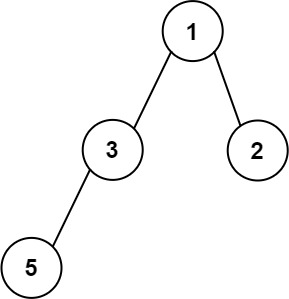
Input: root = [1,3,2,5]
Output: 2
Explanation: The maximum width exists in the second level with length 2 (3,2).
Constraints:
- The number of nodes in the tree is in the range
[1, 3000]. -100 <= Node.val <= 100
Solution
import com_github_leetcode.TreeNode
import java.util.LinkedList
import java.util.Objects
import java.util.Queue
/*
* Example:
* var ti = TreeNode(5)
* var v = ti.`val`
* Definition for a binary tree node.
* class TreeNode(var `val`: Int) {
* var left: TreeNode? = null
* var right: TreeNode? = null
* }
*/
class Solution {
internal class Pair(node: TreeNode, idx: Int) {
var node: TreeNode
var idx: Int
init {
this.node = node
this.idx = idx
}
}
fun widthOfBinaryTree(root: TreeNode): Int {
val q: Queue<Pair> = LinkedList()
q.add(Pair(root, 0))
var res = 1
while (q.isNotEmpty()) {
val qSize = q.size
var lastIdx = 0
var firstIdx = 0
for (i in 0 until qSize) {
val temp = q.poll()
if (i == 0) {
firstIdx = temp.idx
}
if (i == qSize - 1) {
lastIdx = Objects.requireNonNull(temp).idx
}
if (Objects.requireNonNull(temp).node.left != null) {
q.add(Pair(temp.node.left!!, 2 * temp.idx + 1))
}
if (temp.node.right != null) {
q.add(Pair(temp.node.right!!, 2 * temp.idx + 2))
}
}
res = (lastIdx - firstIdx + 1).coerceAtLeast(res)
}
return res
}
}

